El modelo de Markov oculto

El modelo de Markov oculto

• Primero, conocer.

  Hoy vamos a presentar una aplicación sencilla del HMM (modelo de Markov) en las acciones.

  El modelo de Markov oculto, que parece muy sofisticado y no tiene ninguna idea de lo que es, entonces vamos a dar un paso atrás y ver las cadenas de Markov primero.

  Las cadenas de Markov, nombradas así por Andrei Markov (A. A. Markov, 1856-1922), son procesos aleatorios de eventos dissociados de carácter Markov en matemáticas. Dado el conocimiento o la información actual, el pasado (es decir, el estado histórico anterior al presente) no es relevante para predecir el futuro (es decir, el estado futuro posterior al presente).

  

  En este proceso, el desplazamiento de cada estado depende solo de los n estados anteriores, lo que se conoce como un modelo de n estados, en el que n es el número de estados que afectan al desplazamiento. El proceso de Markov más simple es un proceso de un estado, en el que el desplazamiento de cada estado depende solo del estado anterior.

• Dos ejemplos

  La expresión matemática es la siguiente:

  

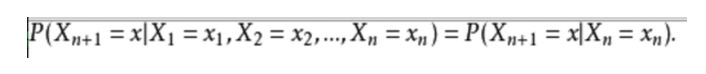
  Demostremos un ejemplo de la vida cotidiana en el que queremos predecir el tiempo futuro en función de las condiciones meteorológicas actuales. Una forma de hacerlo es asumir que cada estado del modelo depende del anterior, el supuesto de Markov, que simplifica enormemente el problema. Por supuesto, este ejemplo también es poco práctico.

  

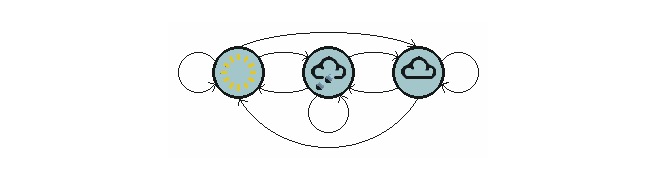
  El gráfico de arriba muestra un modelo del cambio climático.

  Observe que un proceso de primera fase con N estados tiene N2 cambios de estado. La probabilidad de cada cambio es llamada probabilidad de cambio de estado, es decir, la probabilidad de pasar de un estado a otro. Todas estas probabilidades N2 se pueden representar con una matriz de cambio de estado, como en el ejemplo del clima anterior:

  

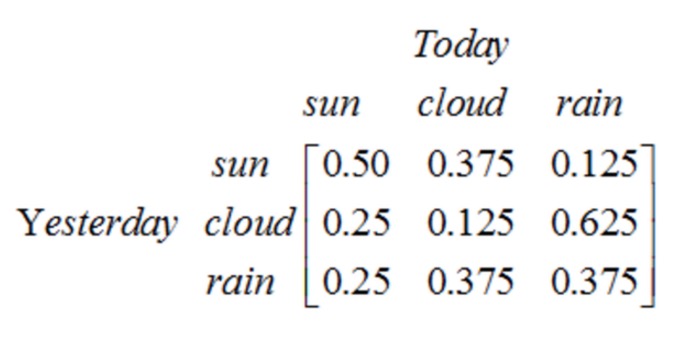
  Esta matriz dice que si ayer ha sido nublado, entonces hay un 25% de probabilidad de que hoy sea un día despejado, un 12.5% de probabilidad de que haya nublado, un 62.5% de probabilidad de que llueva y, obviamente, la suma de cada línea en la matriz es de uno.

  Para iniciar un sistema como este, necesitamos un vector de probabilidad inicial:

  

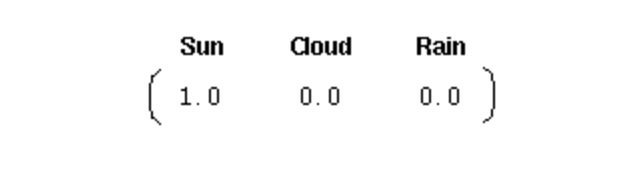
  Este vector indica que el primer día es de día. Hasta aquí, hemos definido las tres partes siguientes para el proceso Markov de la primera etapa anterior:

  El estado: día claro, nublado y lluvia.

  Vector inicial: define la probabilidad del estado del sistema cuando el tiempo es 0.

  Matriz de desplazamiento de estado: probabilidad de cada cambio climático. Todos los sistemas que pueden describirse así son procesos de Markov.

  Sin embargo, ¿qué hacemos cuando los procesos de Markov no son lo suficientemente potentes? En algunos casos, los procesos de Markov no son suficientes para describir los patrones que esperamos encontrar.

  Por ejemplo, en nuestro mercado de valores, si solo observamos el mercado, solo podemos saber el precio del día, la información sobre el volumen de transacciones, etc., pero no sabemos qué estado tiene el mercado de valores en ese momento (bull market, bear market, shock, rebound, etc.), en este caso, tenemos dos conjuntos de estados, un conjunto de estados observables (stock market price trading status, etc.) y un conjunto de estados ocultos (stock market status).

  En estos casos, la secuencia de estados observables y la secuencia de estados ocultos son probables. Así que podemos modelar este tipo de procesos como un proceso de Markov oculto y un conjunto de estados observables relacionados con la probabilidad de este proceso de Markov oculto, el modelo de Markov oculto.

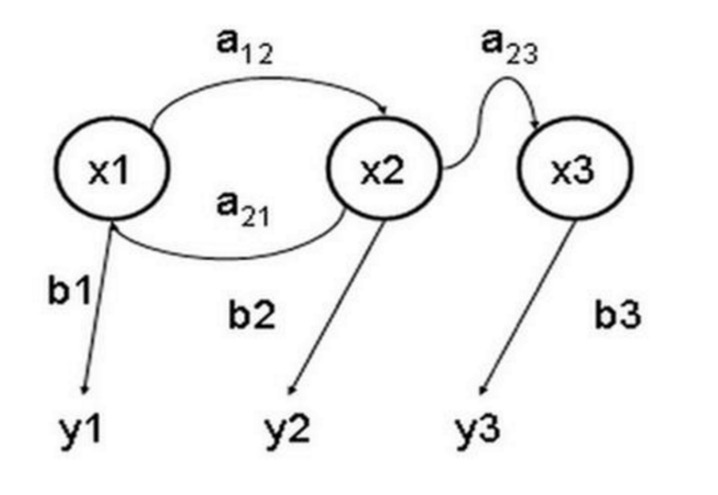
  El modelo oculto de Markov es un modelo estadístico para describir un proceso de Markov que contiene parámetros implicitos desconocidos. Su punto difícil es determinar los parámetros implicados del proceso a partir de los parámetros observables y luego utilizarlos para realizar un análisis adicional. La siguiente figura es un diagrama de transferencia de estado del modelo oculto de Markov de tres estados, donde x representa el estado implicado, y representa la salida observable, a la probabilidad de conversión del estado y b la salida.

  

  Explique esto con el ejemplo de un mazo: supongamos que tengo tres mazos diferentes en mi mano. El primer mazo es nuestro mazo común (llamamos este mazo D6), con 6 caras, y cada cara tiene 1/6 de probabilidad. El segundo mazo es un cuadrado (llamamos este mazo D4), y cada cara tiene 1/4, y el tercer mazo tiene 8 caras (llamamos este mazo D8), y cada cara tiene 1/8, y cada cara tiene 1, 2, 3, 4, 5, 6, 7, 8).

  

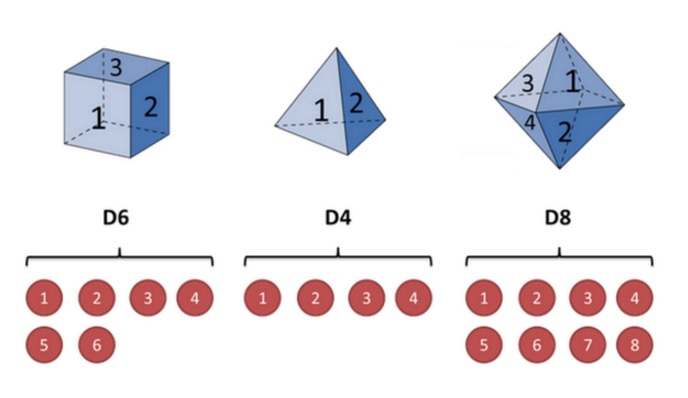
  Supongamos que comenzamos el juego de los dados, primero elegimos uno de los tres dados, y la probabilidad de que cada dado tenga una probabilidad de 1/3. Luego elegimos el dado, obteniendo un número, uno de 1, 2, 3, 4, 5, 6, 7, 8. Repitiendo el proceso continuamente obtendremos una serie de números, cada uno de los cuales es uno de 1, 2, 3, 4, 5, 6, 7, 8.

  Esta serie de números se llama cadena de estado visible. Pero en el modelo de Invisible Markov, no solo tenemos una cadena de estado visible, sino también una cadena de estado implícita. En este ejemplo, la cadena de estado implícita es la secuencia de cuello que usas.

  一般来说，HMM中说到的马尔可夫链其实是指隐含状态链，因为隐含状态（骰子）之间存在转换概率。在我们这个例子里，D6的下一个状态是D4，D6，D8的概率都是1/3。D4，D8的下一个状态是D4，D6，D8的转换概率也都一样是1/3。这样设定是为了最开始容易说清楚，但是我们其实是可以随意设定转换概率的。比如，我们可以这样定义，D6后面不能接D4，D6后面是D6的概率是0.9，是D8的概率是0.1。这样就是一个新的HMM。

  Del mismo modo, aunque no existe una probabilidad de conversión entre los estados visibles, existe una probabilidad entre el estado implícito y el estado visible llamada probabilidad de salida. En nuestro ejemplo, la probabilidad de salida de 1 en el casco de seis caras (D6) es 1/6. La probabilidad de salida de 2, 3, 4, 5, 6 también es 1/6. También podemos hacer otras definiciones de la probabilidad de salida.

  

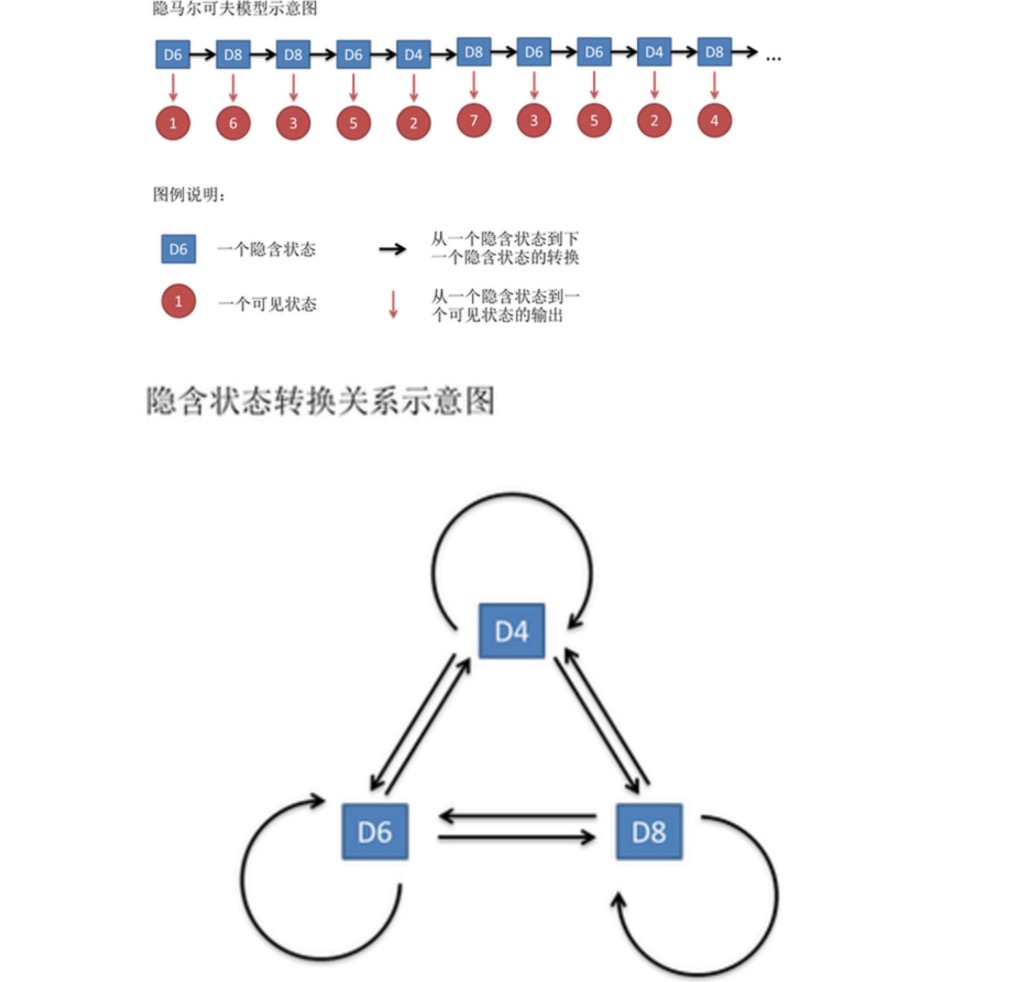
  De hecho, para el HMM, es bastante fácil hacer simulaciones si se conoce de antemano la probabilidad de conversión entre todos los estados implícitos y la probabilidad de salida entre todos los estados implícitos y todos los estados visibles. Pero cuando se aplica el modelo HMM, a menudo se pierde parte de la información, a veces se sabe que hay varios tipos de mazos, qué es cada uno de ellos, pero no se sabe la secuencia de mazos que se producen; a veces solo se ve el resultado de muchos mazos y no se sabe nada del resto.

  Los algoritmos relacionados con el modelo HMM se dividen en tres categorías principales, que resuelven tres problemas:

  • Saber que hay varios monos (cuanto estado implícito hay) y cuál es cada monos (probabilidad de conversión), según el resultado del monos (cadena de estado visible), quiero saber qué monos (cadena de estado implícito) salen cada vez.

  • También se sabe que hay varios tipos de monos (número de estados implícitos), qué es cada tipo de monos (probabilidad de conversión), y en función del resultado del monos (cadena de estados visible), quiero saber la probabilidad de obtener este resultado.

  • Saber que hay varios tipos de monos (número de estados implícitos), no saber qué es cada tipo de monos (probabilidad de conversión), observar el resultado de muchos tipos de monos (cadena de estados visible), y quiero invertir lo que es cada tipo de monos (probabilidad de conversión).

    Si queremos resolver los problemas de las bolsas, necesitamos resolver los problemas 1 y 3, y en el próximo artículo veremos cómo hacerlo.

Transmitido por el columnista de Moneycode