Simulation d'Ornstein-Uhlenbeck avec Python

Dans cet article, nous allons décrire le processus Ornstein-Uhlenbeck, décrire sa formule mathématique, l'implémenter et le simuler à l'aide de Python, et discuter de certaines applications pratiques dans la finance quantitative et les transactions systémiques. Nous allons utiliser un modèle de processus aléatoire plus avancé, appelé processus Ornstein-Uhlenbeck (OU), qui peut être utilisé pour modéliser des séquences de temps qui présentent des comportements de régression de l'égalité.

Quel est le processus d'Ornstein-Uhlenbeck?

Le processus d'Ornstein-Uhlenbeck est un processus aléatoire en temps continu utilisé pour modéliser le comportement de régression des moyennes. Cela signifie que, contrairement à la vague aléatoire standard ou au mouvement de Browne, qui peut dériver à l'infini, le processus d'OU se rétablit souvent à des moyennes à long terme au fil du temps. Mathématiquement, le processus d'OU est la solution d'une équation dérivée aléatoire spécifique (SDE) qui contrôle ce comportement de régression des moyennes.

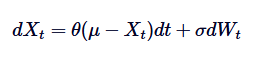
Par exemple, Xt représente un processus aléatoire au temps t, où μ est la moyenne à long terme,θ est la moyenne de régression,δ est la volatilité, et dWt est le processus Wiener ou le mouvement standard de Brownian.

Contexte historique et application

Le procédé Ornstein-Uhlenbeck a été initialement proposé par Leonard Ornstein et George Eugene Uhlenbeck en 1930 pour simuler la vitesse de Brownian motion des particules en présence de friction. Au fil du temps, sa utilité s'est étendue bien au-delà de la physique et a été appliquée dans divers domaines tels que la biologie, la chimie, l'économie et la finance.

Dans la finance quantitative, le processus d'OU est particulièrement utile pour modéliser des phénomènes qui présentent un comportement de régression de l'équation; des exemples notables incluent les taux d'intérêt, les taux de change et la volatilité des marchés financiers. Par exemple, le modèle d'intérêt populaire Vasicek est directement dérivé du processus d'OU.

L'importance de la finance quantitative

Le processus d'Ornstein-Uhlenbeck est essentiel dans la finance quantitative pour les raisons suivantes. Sa nature de régression de l'égalité de valeur le rend naturel pour modéliser les variables financières, qui ne se déplacent pas au hasard, mais tournent autour de fluctuations de la moyenne à long terme stable. Cette caractéristique est essentielle pour la modélisation des taux d'intérêt, où la régression de l'égalité de valeur reflète l'influence des banques centrales sur les taux d'intérêt stables à long terme.

En outre, le processus d'OU est utilisé dans les modèles de prix d'actifs (y compris la valorisation des dérivés) et les stratégies de gestion des risques. Il peut également servir de bloc de construction à des modèles plus complexes, tels que le modèle Cox-Ingersoll-Ross (CIR), qui étend le processus d'OU à la modélisation des taux d'intérêt non négatifs.

Principales caractéristiques et intuitions

Les principales caractéristiques du processus Ornstein-Uhlenbeck peuvent être résumées comme suit:

• Les valeurs moyennes de régression sont:Le processus OU a tendance à revenir à la moyenne à long terme μ. Cela contraste fortement avec des processus tels que le mouvement de Brown, qui n'exerce pas cette tendance.
• La volatilité:Le paramètre δ contrôle le niveau de hasard ou de volatilité dans le processus. Plus la volatilité est élevée, plus le processus dévie de la moyenne avant la régression.
• La vitesse de retour:Le paramètre θ détermine la vitesse à laquelle le processus retourne aux moyennes.
• La stabilité:Le processus de l'OU est calme, ce qui signifie que ses caractéristiques statistiques ne changent pas avec le temps.

Intuitivement, vous pouvez considérer le processus d'Ornstein-Uhlenbeck comme une modélisation du comportement du muscle pelvien qui s'étire autour de la moyenne. Bien que le processus puisse s'écarter de l'équilibre en raison de fluctuations aléatoires, la force de traction du muscle pelvien (similaire à la régression de l'équilibre) assure qu'il revient finalement à l'équilibre.

Comparaison avec d'autres processus aléatoires

Comme le processus OU est étroitement lié à la modélisation de divers phénomènes financiers, il est souvent comparé à d'autres processus aléatoires (tels que le mouvement de Brown et le mouvement géométrique de Brown (GBM)).

Comparé au GBM, qui est généralement utilisé pour modéliser les prix des actions et qui contient des éléments de dérive et de fluctuation, le processus OU ne montre pas de croissance indicielle, mais plutôt une oscillation autour de sa moyenne. Le GBM est plus approprié pour modéliser des quantités qui augmentent avec le temps, tandis que le processus OU est très approprié pour modéliser des variables qui présentent des caractéristiques de régression de la moyenne.

Exemples de finance quantitative

Le procédé Ornstein-Uhlenbec a de nombreuses applications dans le domaine financier, en particulier dans les scénarios de modélisation où la régression des moyennes est une caractéristique clé. Nous allons discuter ci-dessous de quelques-uns des cas d'utilisation les plus courants.

Modélisation des taux d'intérêt

L'une des applications les plus remarquables du processus OU est la modélisation des taux d'intérêt, en particulier dans le cadre du modèle de Vasicek. Le modèle de Vasicek suppose que les taux d'intérêt suivent le processus OU, c'est-à-dire que les taux d'intérêt reviennent souvent à leur moyenne à long terme au fil du temps. Cette caractéristique est cruciale pour un comportement d'analogie précise des taux d'intérêt, car les taux d'intérêt ne fluctuent souvent pas indéfiniment, mais se situent près du niveau moyen, sous l'influence des conditions économiques.

Prix des actifs

Dans la valorisation des actifs, en particulier des titres à revenu fixe, le processus OU est souvent utilisé pour simuler l'évolution des taux de rendement des obligations. La nature de la régression de l'OU assure que les taux de rendement ne s'écartent pas trop de leur moyenne historique, ce qui est conforme au comportement observé du marché.

Stratégie de couplage

L'appariement des transactions est une stratégie neutre sur le marché qui implique l'établissement d'une position de contrepartie entre deux actifs concernés. Dans ce cas, le processus OU est particulièrement utile car il permet de modéliser la différence de prix entre les deux actifs, qui est généralement une régression de la valeur moyenne.

Par exemple, si le décalage entre deux contrats s'élargit au-delà d'un certain seuil, les traders peuvent éliminer des contrats performants et éliminer des contrats performants, en espérant que le décalage redevienne à sa moyenne historique, afin de réaliser un profit en cas d'inversion.

Réponse de Ornstein-Uhlenbeck SDE

La formule de l'équation différentielle du processus Ornstein-Uhlenbeck est la base de sa résolution. Pour résoudre cette SDE, nous avons utilisé le facteur d'intégration.

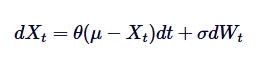
Donc nous allons commencer par multiplier les deux côtés par des facteurs de multiplication. :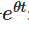

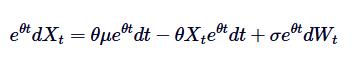
Remarquez que si on ajoute les deux côtés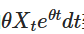La différence est donc la différence de la multiplication:

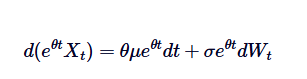
Si on multiplie les deux côtés de 0 à t, on obtient:

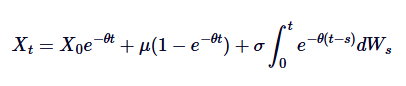
Il s'agit d'une solution générale du SDE d'Ornstein-Uhlenbeck.

Les solutions explicites déduites ci-dessus ont plusieurs significations importantes.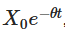Indique que la valeur initiale décline avec le temps, indiquant comment le processus s'évanouit et oublie son point de départ.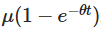Le processus est indiqué comme tendant à la moyenne au fil du temps μ. Le troisième élément introduit la randomisation, dans laquelle les composantes impliquées dans le processus Wiener expliquent les fluctuations aléatoires.

Cette solution met l'accent sur l'équilibre entre le comportement de régression de l'égalité de certitude et les fractions aléatoires entraînées par le mouvement de Brownian. Comprendre cette solution est essentiel pour simuler efficacement les processus OU, comme indiqué ci-dessous.

Liens avec d'autres processus aléatoires

Le processus d'Ornstein-Uhlenbeck a plusieurs liens importants avec d'autres processus aléatoires bien connus (y compris le mouvement de Brown et le modèle de Vasicek).

Les liens avec le mouvement Brown

Le processus d'Ornstein-Uhlenbeck peut être considéré comme une version de la régression moyenne du mouvement de Browne. Le mouvement de Browne décrit un processus de tendance avec une augmentation indépendante et aucune régression moyenne, tandis que le processus d'OU introduit une régression moyenne en modifiant le mouvement de Browne à l'aide d'un élément de dérive, ce qui ramène le processus à sa valeur centrale. Mathématiquement, si nous définissons th = 0, le processus d'OU est simplifié en mouvement de Browne standard avec des fluctuations:

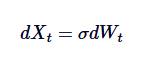
Ainsi, le mouvement de Brown est une exception au processus OU, correspondant à l'absence de régression des moyennes.

La relation avec le modèle Vasicek

Le modèle de Vasicek est largement utilisé dans la modélisation des taux d'intérêt, essentiellement pour l'application du processus Ornstein-Uhlenbeck dans l'évolution des taux d'intérêt. Le modèle de Vasicek suppose que le taux d'intérêt suit le processus OU, dans lequel le SDE est défini comme:

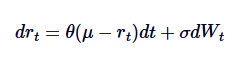
Parmi ceux-ci, r représente le taux d'intérêt à court terme, l'interprétation des paramètres θ, μ et δ est similaire à celle du processus OU. Le modèle Vasicek est capable de produire des chemins de retour à l'équilibre des taux d'intérêt, ce qui est l'un de ses principaux avantages dans la modélisation financière.

Comprendre ces relations permet de mieux comprendre comment les processus OU sont utilisés dans différents environnements, en particulier dans le domaine financier.

Simulation du processus Ornstein-Uhlenbeck avec Python

Dans cette section, nous allons explorer comment utiliser Python pour simuler le processus Ornstein-Uhlenbeck (OU). Cela implique d'utiliser la discrétion d'Euler-Maruyama pour discréter les équations définies par le processus OU (SDE).

Décentralisation de la SDE

Nous allons passer en revue les formules mathématiques de SDE ci-dessus et résumer chaque terme:

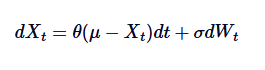
Il y en a une.

• Xt est la valeur du processus au moment t.
• θ est la vitesse de retour de la moyenne.
• μ est la moyenne à long terme du processus.
• δ est le paramètre de fluctuation.
• dWt représente l'incrémentation du processus Wiener (mouvement standard de Brown).

Pour simuler ce processus sur un ordinateur, nous avons besoin de découpler les SDE en temps continu. Une méthode couramment utilisée est la découplage d'Euler-Maruyama, qui prend en compte les petites pauses de temps découpées.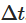La forme dissociée du processus Ornstein-Uhlenbeck est donnée par:

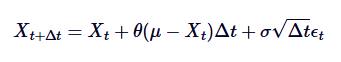
Il y en a une.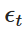est une variable aléatoire extraite d'une distribution normale standard (i.e.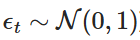Cette dissociation nous permet de calculer la valeur de Xt de manière irrégulière au fil du temps, simulant ainsi le comportement du processus OU.

Mise en œuvre de Python

Maintenant, nous allons réaliser un processus Ornstein-Uhlenbeck décentralisé en Python. Dans le texte ci-dessous, nous n'utilisons que NumPy et la bibliothèque Python Matplotlib.

Tout d'abord, nous importons NumPy et Matplotlib de manière standard. Ensuite, nous spécifions tous les paramètres pour le modèle OU. Ensuite, nous prépartissons un ensemble NumPy de longueur N pour l'ajouter après avoir calculé le chemin de l'OU. Ensuite, nous répétons les étapes N-1 (étape 1 est la condition initiale indiquée X0), simulons l'augmentation aléatoire DW, puis calculons la prochaine génération du chemin de l'OU en fonction de la formule mathématique ci-dessus. Enfin, nous utilisons Matplotlib pour tracer l'histoire du chemin.

import numpy as np
import matplotlib.pyplot as plt

# Parameters for the OU process
theta = 0.7      # Speed of mean reversion
mu = 0.0         # Long-term mean
sigma = 0.3      # Volatility
X0 = 1.0         # Initial value
T = 10.0         # Total time
dt = 0.01        # Time step
N = int(T / dt)  # Number of time steps

# Pre-allocate array for efficiency
X = np.zeros(N)
X[0] = X0

# Generate the OU process
for t in range(1, N):
    dW = np.sqrt(dt) * np.random.normal(0, 1)
    X[t] = X[t-1] + theta * (mu - X[t-1]) * dt + sigma * dW

# Plot the result
plt.plot(np.linspace(0, T, N), X)
plt.title("Ornstein-Uhlenbeck Process Simulation")
plt.xlabel("Time")
plt.ylabel("X(t)")
plt.show()

Le résultat du dessin est le suivant:

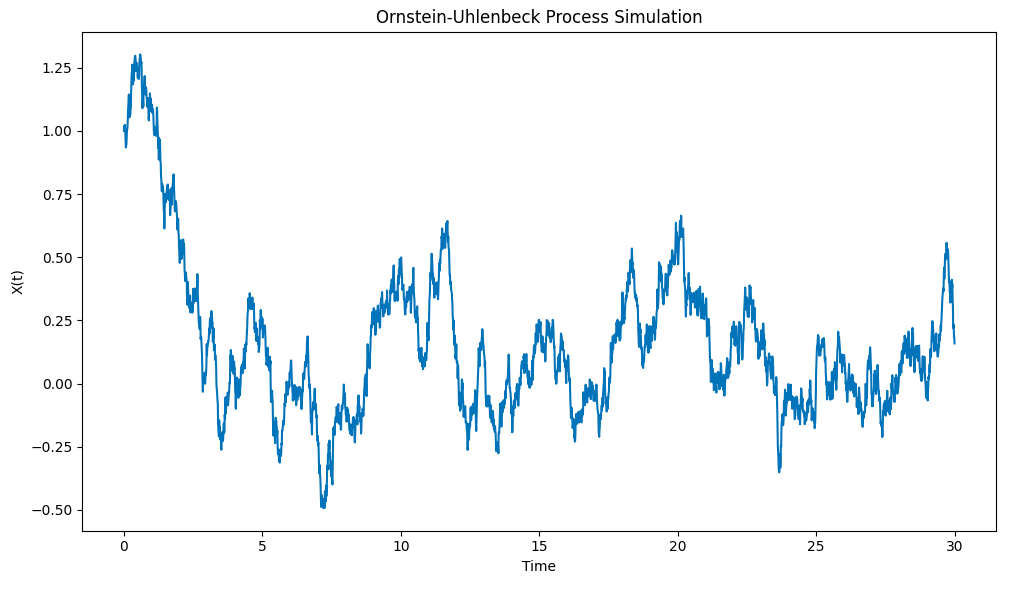
Simulation du processus Ornstein-Uhlenbeck avec Python

Notez comment le processus tire rapidement le plomb de la condition initiale X0=1 à la valeur moyenne μ=0, puis il montre une tendance à revenir à cette valeur moyenne lorsqu'il s'écarte de cette valeur moyenne.

Résumé et étapes à suivre

Dans cet article, nous avons présenté un aperçu des processus Ornstein-Uhlenbeck, décrit leurs formules mathématiques et fourni des implémentations de base de Python pour simuler des versions discrètes de SDE en temps continu. Dans les articles suivants, nous étudierons les SDE plus complexes construits à partir de processus OU et comment ils peuvent être utilisés dans les applications de négociation systémique et de tarification des dérivés.

Le code complet

# OU process simulation

import numpy as np
import matplotlib.pyplot as plt

# Parameters for the OU process
theta = 0.7      # Speed of mean reversion
mu = 0.0         # Long-term mean
sigma = 0.3      # Volatility
X0 = 1.0         # Initial value
T = 30.0         # Total time
dt = 0.01        # Time step
N = int(T / dt)  # Number of time steps

# Pre-allocate array for efficiency
X = np.zeros(N)
X[0] = X0

# Generate the OU process
for t in range(1, N):
    dW = np.sqrt(dt) * np.random.normal(0, 1)
    X[t] = X[t-1] + theta * (mu - X[t-1]) * dt + sigma * dW

# Plot the result
plt.plot(np.linspace(0, T, N), X)
plt.title("Ornstein-Uhlenbeck Process Simulation")
plt.xlabel("Time")
plt.ylabel("X(t)")
plt.show()

Le lien vers l'original:https://www.quantstart.com/articles/ornstein-uhlenbeck-simulation-with-python/