Le modèle de Markov

Le modèle de Markov

• Première étape:

  Aujourd'hui, nous allons vous présenter une application simple de HMM (le modèle de Markov) sur les actions.

  Le modèle de Markov, qui semble très sophistiqué, ne sait pas ce que c'est, alors prenons un peu de recul et regardons la chaîne de Markov.

  Les chaînes de Markov, nommées d'après Andreï Markov (A. A. Markov, 1856-1922), sont des processus aléatoires d'événements discrets de nature markovite en mathématiques. Dans le cas de connaissances ou d'informations actuelles, le passé (c'est-à-dire l'état historique antérieur au présent) est sans rapport avec le futur (c'est-à-dire l'état futur après le présent) prévu.

  

  Dans ce processus, la transition de chaque état dépend uniquement des n états précédents, ce qui est appelé un modèle à n niveaux, où n est le nombre d'états affectés par la transition. Le processus de Markov le plus simple est un processus de première étape, où la transition de chaque état dépend uniquement de l'état qui l'a précédé.

• Deuxième exemple

  L'expression mathématique est la suivante:

  

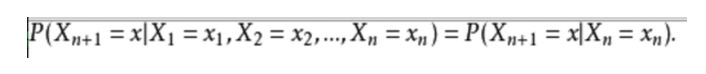
  Prenons un exemple de la vie quotidienne où nous voulons prédire les conditions météorologiques futures en fonction des conditions météorologiques actuelles. Une façon de procéder est de supposer que chaque état de ce modèle ne dépend que de l'état précédent, c'est-à-dire de l'hypothèse de Markov, qui simplifie considérablement le problème.

  

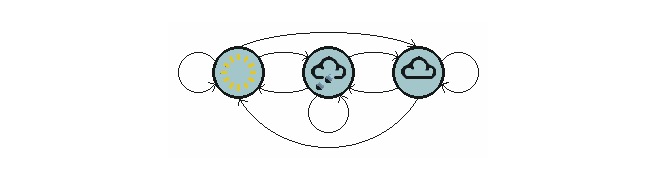
  Le graphique ci-dessus montre un modèle de météo qui se déplace.

  Notez qu'un processus de phase 1 contenant N états a N2 transitions d'état. La probabilité de chaque transition est appelée probabilité de transition d'état, c'est-à-dire la probabilité de transition d'un état à un autre. Toutes ces probabilités N2 peuvent être représentées par une matrice de transition d'état, comme dans l'exemple météorologique ci-dessus:

  

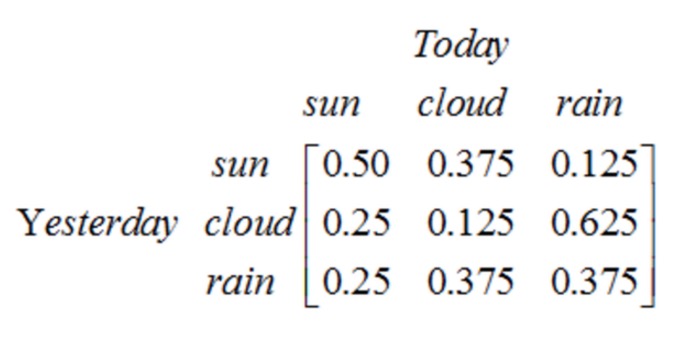
  Cette matrice indique que si hier il y a eu un temps nuageux, il y a 25% de chances que ce soit un jour clair aujourd'hui, 12,5% de probabilité que ce soit un temps nuageux et 62,5% de probabilité qu'il pleuve.

  Pour initialement un tel système, nous avons besoin d'un vecteur de probabilité initial:

  

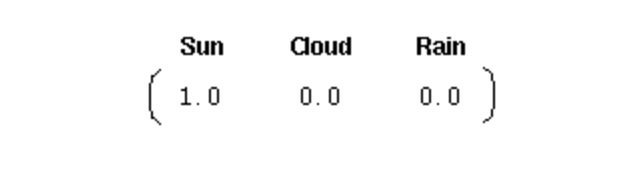
  Ce vecteur indique que le premier jour est clair. Jusque-là, nous avons défini les trois parties suivantes pour le processus de Markov de la première étape ci-dessus:

  La situation: temps clair, nuageux et pluie.

  Vecteur initial: définit la probabilité de l'état du système à 0 temps.

  Matrice de transfert d'état: probabilité de chaque transformation météorologique. Tous les systèmes qui peuvent être décrits de cette façon sont des processus de Markov.

  Cependant, que faire lorsque le processus de Markov n'est pas assez puissant? Dans certains cas, le processus de Markov n'est pas assez puissant pour décrire les modèles que nous espérons trouver.

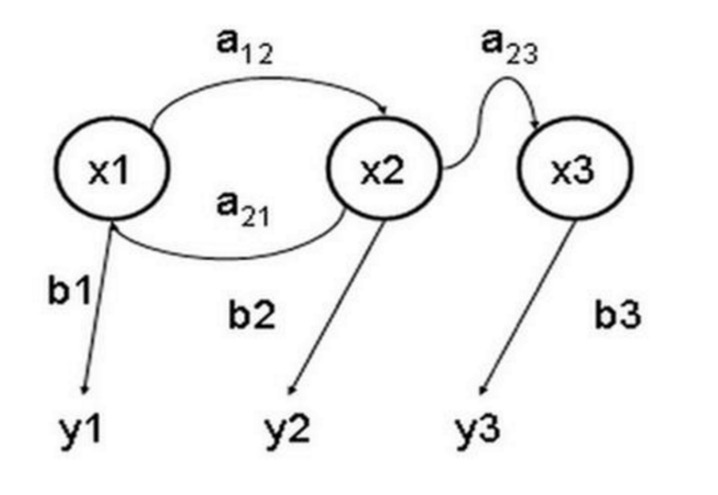
  Par exemple, dans notre bourse, si nous observons le marché, nous ne pouvons connaître que les prix, les volumes, etc. du jour, mais nous ne savons pas quel est l'état du marché en ce moment (bull market, bear market, shock, rebond, etc.), dans ce cas, nous avons deux ensembles d'états, un ensemble d'états observables (stock market price trading status, etc.) et un ensemble d'états cachés (stock market status). Nous souhaitons trouver un algorithme qui puisse prédire l'état du marché en fonction de l'état du prix du marché et de l'hypothèse de Markov.

  Dans ces cas ci-dessus, les séquences d'états observables et les séquences d'états cachées sont probables. Nous pouvons donc modéliser ce type de processus comme un processus Markov caché et un ensemble d'états observables et liés à la probabilité de ce processus Markov caché, le modèle de Markov caché.

  Le modèle caché de Markov est un modèle statistique utilisé pour décrire un processus de Markov contenant des paramètres inconnus implicites. La difficulté est de déterminer les paramètres implicites du processus à partir des paramètres observables, puis d'utiliser ces paramètres pour une analyse plus approfondie.

  

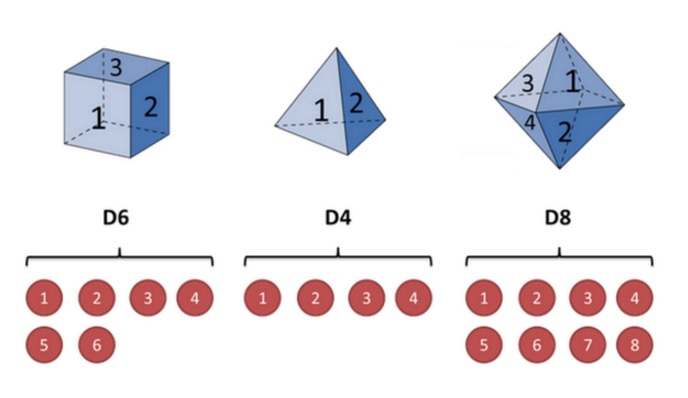
  Expliquez-le avec l'exemple d'un casque: supposons que j'ai trois casques différents dans ma main. Le premier casque est notre casque ordinaire (appelons ce casque D6), avec 6 faces, chaque face (appelons 1, 2, 3, 4, 5, 6) a une probabilité de 1/6. Le second casque est un quadrilatère (appelons ce casque D4), chaque face (appelons 1, 2, 3, 4) a une probabilité de 1/4. Le troisième casque a huit faces (appelons ce casque D8), chaque face (appelons 1, 2, 3, 4, 5, 6, 7, 8) a une probabilité de 1/8.

  

  Supposons que nous commencions le jeu en choisissant l'un des trois premiers et que la probabilité de choisir un de ces trois numéros est de 1/3; puis nous faisons le jeu et nous obtenons un nombre, 1, 2, 3, 4, 5, 6, 7, 8; répétons ce processus sans arrêt et nous obtenons une série de numéros, chaque numéro est un des 1, 2, 3, 4, 5, 6, 7, 8; par exemple, nous pouvons obtenir une série de numéros comme celle-ci:

  Cette série de chiffres est appelée chaîne d'état visible. Mais dans le modèle de Markov, nous avons non seulement une chaîne d'état visible, mais aussi une chaîne d'état implicite. Dans cet exemple, la chaîne d'état implicite est la séquence de la souris que vous utilisez.

  一般来说，HMM中说到的马尔可夫链其实是指隐含状态链，因为隐含状态（骰子）之间存在转换概率。在我们这个例子里，D6的下一个状态是D4，D6，D8的概率都是1/3。D4，D8的下一个状态是D4，D6，D8的转换概率也都一样是1/3。这样设定是为了最开始容易说清楚，但是我们其实是可以随意设定转换概率的。比如，我们可以这样定义，D6后面不能接D4，D6后面是D6的概率是0.9，是D8的概率是0.1。这样就是一个新的HMM。

  De même, bien qu'il n'y ait pas de probabilité de conversion entre les états visibles, il existe une probabilité entre les états implicites et les états visibles appelée probabilité de sortie. Dans notre exemple, la probabilité de sortie d'un hexagone (D6) est de 1/6. La probabilité de sortie d'un 2, 3, 4, 5, 6 est également de 1/6.

  

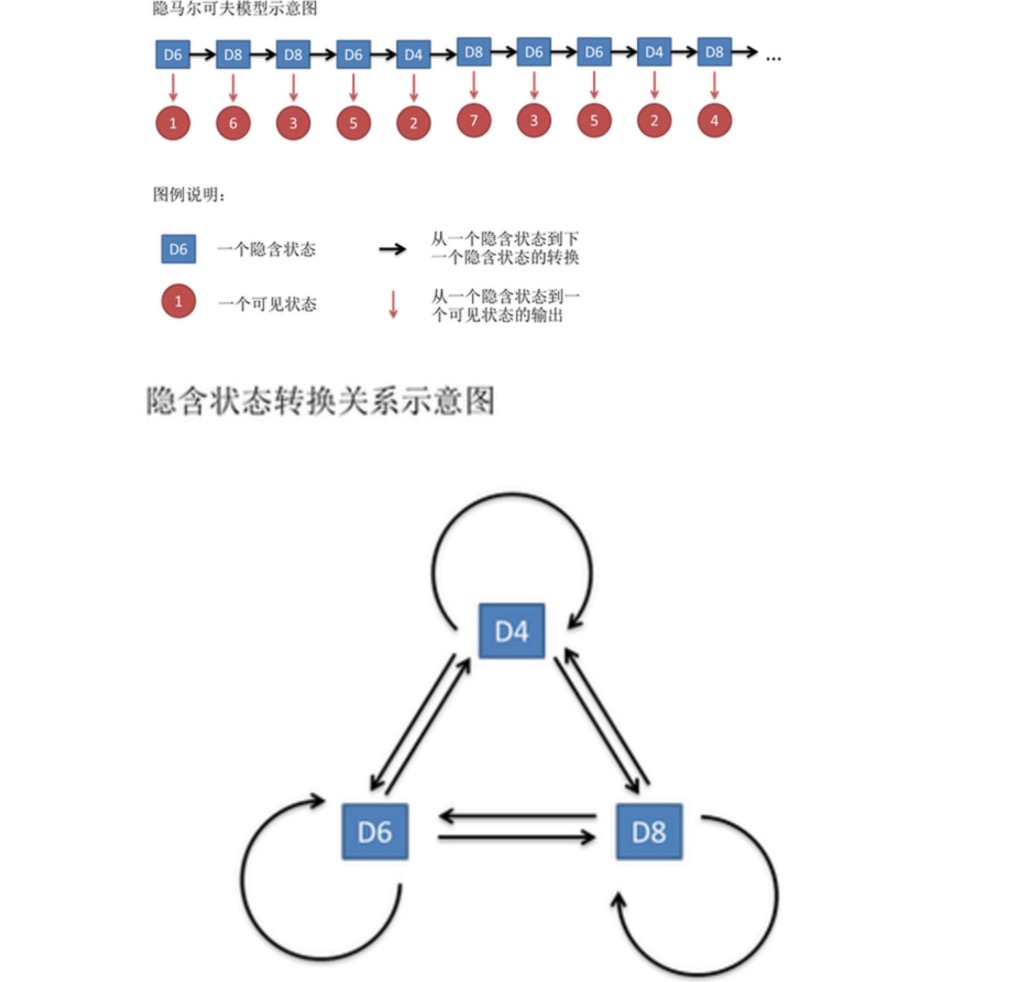
  En fait, pour HMM, il est assez facile de faire des simulations si l'on connaît à l'avance la probabilité de conversion entre tous les états implicites et la probabilité de sortie entre tous les états implicits et tous les états visibles. Mais lorsque l'on applique le modèle HMM, on manque souvent une partie de l'information. Parfois, on sait qu'il y a plusieurs ensembles, quels sont les ensembles, mais on ne sait pas quelle séquence de ensembles est produite.

  Les algorithmes associés aux modèles HMM sont principalement classés en trois catégories, et résolvent respectivement trois problèmes:

  • Sachant qu'il y a plusieurs types de soucoupes (nombre d'états implicites) et ce que chaque type de soucoupes est (probabilité de conversion), je veux savoir quel type de soucoupes sortent à chaque fois en fonction des résultats obtenus (chaîne d'état visible).

  • Il y a plusieurs types de soucoupes (nombre d'états implicites), quelle est la probabilité de chaque type de soucoupée (probabilité de conversion), et je veux savoir quelle est la probabilité de ce type de soucoupée en fonction du résultat (chaîne d'état visible).

  • Sachant qu'il y a plusieurs types de soucoupes (nombre d'états implicites), ne sachant pas ce qu'est chaque type de soucoupée (probabilité de conversion), observant le résultat de plusieurs types de soucoupes (chaîne d'état visible), je veux inverser ce que sont ces types de soucoupes (probabilité de conversion).

    Si nous voulons résoudre le problème de la bourse, nous devons résoudre le problème 1 et le problème 3.

Traduit de l'article de l'auteur de Moneycode