Model Markov yang tersembunyi

Model Markov yang tersembunyi

• Pertama, mengenal

  Hari ini kita akan membahas tentang aplikasi sederhana dari HMM (Markov Model) pada saham.

  Model Markov yang tersembunyi, yang kedengarannya sangat canggih, tidak tahu apa itu, jadi mari kita mundur dan lihat rantai Markov terlebih dahulu.

  Rantai Markov, yang dinamai setelah Andrey Markov (A. A. Markov, 1856-1922), adalah suatu proses acak dari peristiwa terpencil yang memiliki sifat Markov dalam matematika. Dalam hal pengetahuan atau informasi saat ini, masa lalu (yaitu keadaan sejarah sebelum saat ini) tidak relevan untuk memprediksi masa depan (yaitu keadaan masa depan setelah saat ini).

  

  Dalam proses ini, pergeseran setiap negara hanya bergantung pada n negara sebelumnya, proses ini disebut model satu tingkat n, di mana n adalah jumlah negara yang mempengaruhi pergeseran. Proses Markov termudah adalah proses tingkat satu, dimana pergeseran setiap negara hanya bergantung pada satu negara sebelumnya.

• Contoh kedua:

  Dengan menggunakan ekspresi matematis, ini terlihat seperti berikut:

  

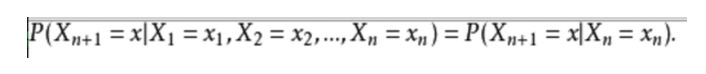
  Untuk memberikan contoh dari kehidupan sehari-hari, kita ingin memprediksi kondisi cuaca di masa depan berdasarkan kondisi cuaca saat ini. Salah satu cara adalah dengan mengasumsikan bahwa setiap keadaan dalam model ini hanya bergantung pada keadaan sebelumnya, yaitu hipotesis Markov, hipotesis yang sangat menyederhanakan masalah ini. Tentu saja, contoh ini juga agak tidak praktis.

  

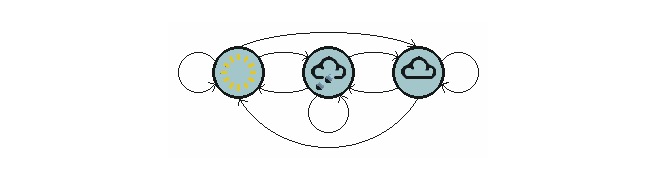
  Gambar di atas menunjukkan model perubahan cuaca.

  Perhatikan bahwa proses tahap pertama yang berisi N keadaan memiliki N2 pergeseran keadaan. Setiap kemungkinan pergeseran disebut probabilitas pergeseran keadaan, yaitu probabilitas pergeseran dari satu keadaan ke keadaan lain. Semua probabilitas N2 ini dapat diwakili dengan sebuah matriks pergeseran keadaan, seperti di contoh cuaca di atas:

  

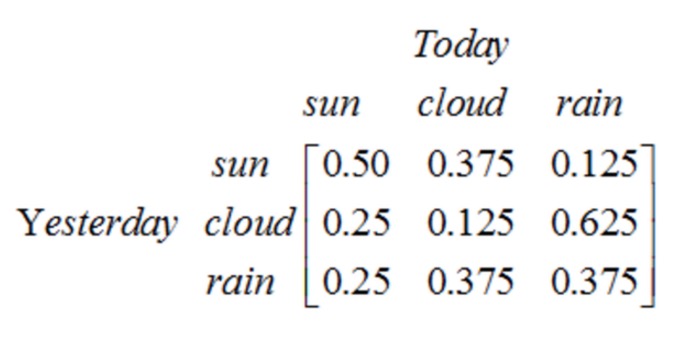
  Matriks ini menyatakan bahwa jika hari kemarin mendung, maka 25% kemungkinan hari ini cerah, 12,5% kemungkinan mendung, 62,5% kemungkinan hujan, dan jelas, setiap baris dalam matriks memiliki jumlah 1.

  Untuk menginisialisasi sistem seperti ini, kita membutuhkan vektor probabilitas awal:

  

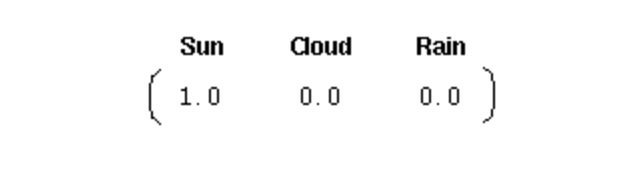
  Vektor ini menunjukkan bahwa hari pertama adalah hari yang cerah. Di sini, kita telah mendefinisikan tiga bagian berikut untuk proses Markov tahap satu di atas:

  Status: Cerah, mendung dan hujan.

  Vektor awal: mendefinisikan probabilitas keadaan sistem pada saat waktu adalah 0.

  Matriks pergeseran keadaan: Probabilitas setiap pergeseran cuaca. Semua sistem yang dapat digambarkan seperti ini adalah proses Markov.

  Namun, apa yang harus kita lakukan ketika proses Markov tidak cukup kuat? Dalam beberapa kasus, proses Markov tidak cukup untuk menggambarkan pola yang ingin kita temukan.

  Misalnya pasar saham kita, jika kita hanya mengamati pasar, kita hanya dapat mengetahui harga, volume, dan lain-lain pada hari itu, tetapi tidak tahu apa keadaan pasar saham saat ini (bull market, bear market, shock, rebound, dan lain-lain), dalam hal ini kita memiliki dua set keadaan, satu set keadaan yang dapat diamati (stock market price trading status, dan lain-lain) dan satu set keadaan tersembunyi (stock market status); kita ingin menemukan algoritme yang dapat memprediksi keadaan pasar saham berdasarkan kondisi harga saham dan asumsi Markov.

  Dalam kasus-kasus di atas, urutan keadaan yang dapat diamati dan urutan keadaan yang tersembunyi terkait kemungkinan. Jadi kita dapat memodelkan proses jenis ini sebagai proses Markov yang tersembunyi dan himpunan keadaan yang terkait dan dapat diamati dengan probabilitas proses Markov yang tersembunyi ini, yaitu model Markov tersembunyi.

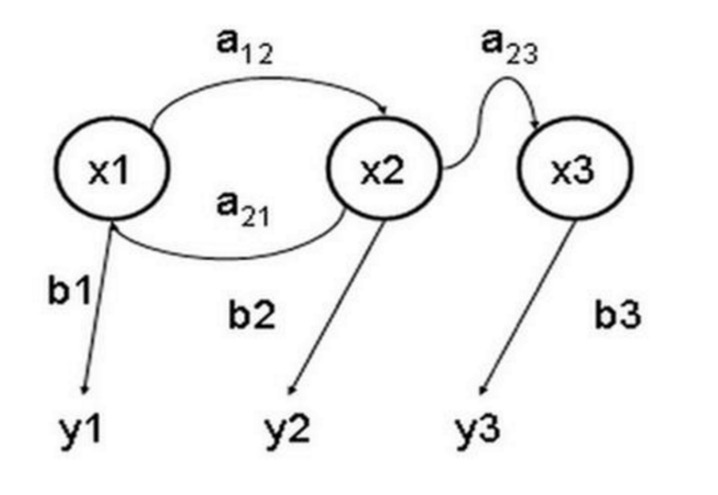
  Model Markov yang tersembunyi adalah model statistik yang digunakan untuk menggambarkan proses Markov yang mengandung parameter yang tidak diketahui secara implisit. Sulitnya adalah menentukan parameter implisit dari proses tersebut dari parameter yang dapat diamati, dan kemudian menggunakan parameter tersebut untuk analisis lebih lanjut. Gambar berikut adalah perpindahan transisi keadaan model Markov yang tersembunyi dalam tiga keadaan, di mana x menunjukkan keadaan implisit, y menunjukkan hasil yang dapat diamati, a menunjukkan kemungkinan konversi keadaan, dan b menunjukkan kemungkinan output.

  

  Sebagai contoh, pertimbangkan sebuah dompet. Misalkan saya memiliki tiga dompet yang berbeda di tangan saya. Dompet pertama adalah dompet biasa kami (menyebut dompet ini D6), dengan 6 sisi, dan setiap sisi (menyebut 1, 2, 3, 4, 5, 6) memiliki probabilitas 1/6. Dompet kedua adalah empat sisi (menyebut dompet ini D4), dan setiap sisi (menyebut 1, 2, 3, 4) memiliki probabilitas 1/4. Dompet ketiga memiliki delapan sisi (menyebut dompet ini D8), dan setiap sisi (menyebut 1, 2, 3, 4, 5, 6, 7, 8) memiliki probabilitas 1/8.

  

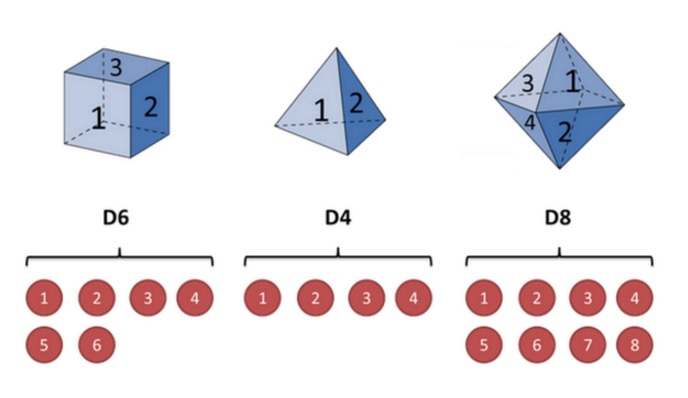
  Misalkan kita mulai dengan dadu, kita pilih satu dari tiga dadu, dan kita pilih satu dari tiga dadu, dan kemungkinan setiap dadu adalah 1/3. Kemudian kita pilih dadu, dan kita mendapatkan satu angka, 1, 2, 3, 4, 5, 6, 7, 8. Mengulangi proses ini terus-menerus, kita akan mendapatkan serangkaian angka, dan setiap angka adalah 1, 2, 3, 4, 5, 6, 7, 8.

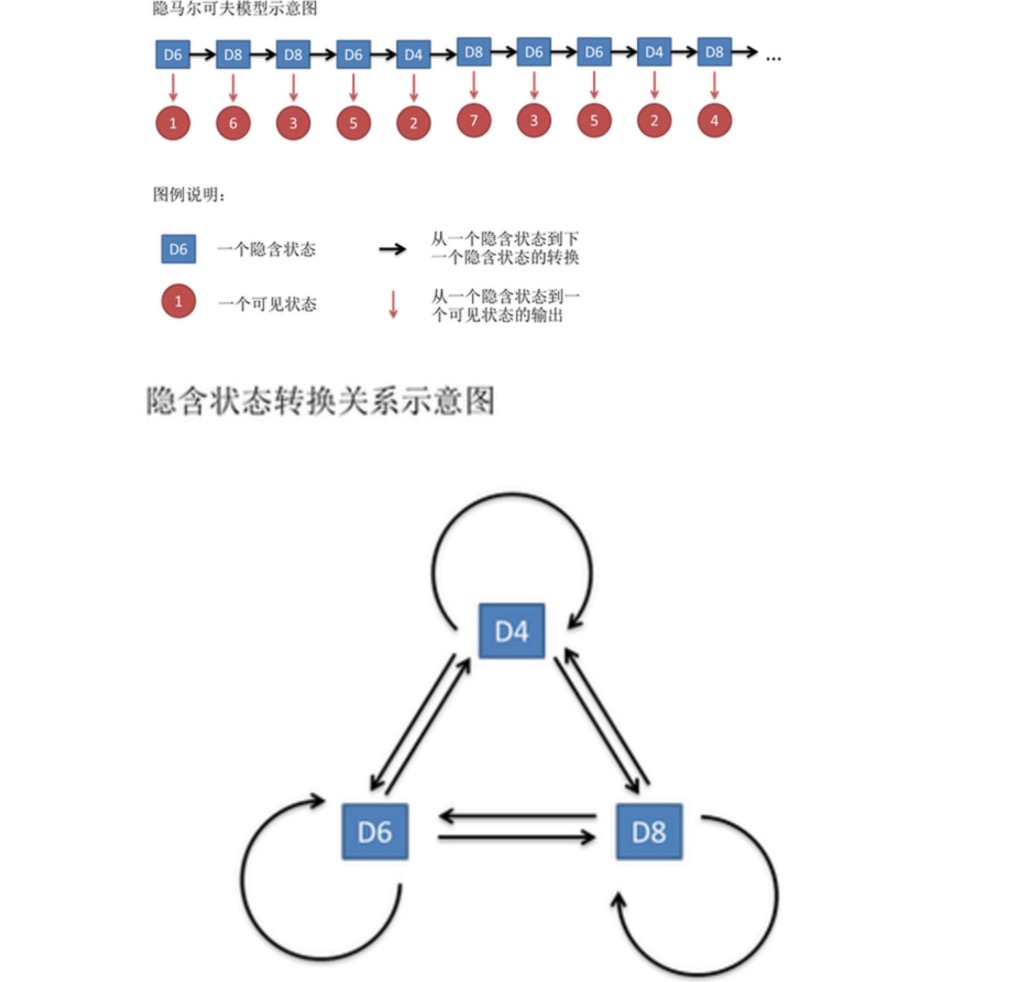
  Rangkaian angka ini disebut rantai keadaan yang terlihat. Namun dalam model Markov yang tersembunyi, kita tidak hanya memiliki rantai keadaan yang terlihat, kita juga memiliki rantai keadaan yang tersirat. Dalam contoh ini, rantai keadaan tersirat adalah rantai yang Anda gunakan. Misalnya, rantai keadaan tersirat mungkin D4 D6 D8 D6 D4 D8 D6 D6 D6 D4.

  一般来说，HMM中说到的马尔可夫链其实是指隐含状态链，因为隐含状态（骰子）之间存在转换概率。在我们这个例子里，D6的下一个状态是D4，D6，D8的概率都是1/3。D4，D8的下一个状态是D4，D6，D8的转换概率也都一样是1/3。这样设定是为了最开始容易说清楚，但是我们其实是可以随意设定转换概率的。比如，我们可以这样定义，D6后面不能接D4，D6后面是D6的概率是0.9，是D8的概率是0.1。这样就是一个新的HMM。

  Demikian pula, meskipun tidak ada kemungkinan konversi antara keadaan yang terlihat, ada probabilitas antara keadaan tersirat dan keadaan yang terlihat yang disebut probabilitas output. Dalam contoh kita, kemungkinan output dari dadu enam sisi (D6) menghasilkan 1 adalah 1/6. Kemungkinan menghasilkan 2, 3, 4, 5, 6 juga 1/6. Kita juga dapat membuat definisi lain tentang kemungkinan output.

  

  Untuk HMM, melakukan simulasi cukup mudah jika Anda tahu terlebih dahulu kemungkinan konversi antara semua keadaan tersirat dan kemungkinan output antara semua keadaan tersirat ke semua keadaan yang terlihat. Tetapi ketika menggunakan model HMM, seringkali ada sebagian informasi yang hilang, kadang-kadang Anda tahu ada beberapa jenis kerucut, apa masing-masing kerucut, tetapi tidak tahu urutan kerucut yang keluar; kadang-kadang Anda hanya melihat banyak hasil kerucut, dan yang tersisa tidak tahu apa-apa.

  Algoritma yang terkait dengan model HMM dibagi menjadi tiga kategori, masing-masing memecahkan tiga masalah:

  • Mengetahui bahwa ada beberapa jenis monkey (jumlah keadaan tersirat), apa setiap jenis monkey (probabilitas konversi), dan berdasarkan hasil monkey (rantai keadaan yang terlihat), saya ingin tahu jenis monkey (rantai keadaan tersirat) yang muncul setiap kali monkey (rantai keadaan tersirat) keluar.

  • Juga tahu bahwa ada beberapa jenis monkey (jumlah negara tersirat), apa kemungkinan setiap monkey (kemungkinan konversi), dan berdasarkan hasil monkey (rantai negara yang terlihat), saya ingin tahu kemungkinan hasil monkey ini.

  • Mengetahui bahwa ada beberapa jenis monkey (jumlah negara tersirat), tidak tahu apa setiap jenis monkey (probabilitas konversi), mengamati hasil dari banyak monkey (rantai negara yang terlihat), saya ingin membalikkan apa setiap jenis monkey (probabilitas konversi).

    Jika kita ingin menyelesaikan masalah di pasar saham di atas, kita perlu menyelesaikan masalah 1 dan 3, dan di artikel berikutnya kita akan melihat bagaimana hal itu bisa dilakukan.

Dikutip dari Moneycode