Pemahaman Intuitif tentang Kointegrasi

Panduan: Artikel ini bertujuan untuk memperkenalkan konsep integrasi secara intuitif, membantu Anda memahami makna dasarnya, motivasi yang dikemukakan oleh konsep ini, dan skenario aplikasi yang sederhana.

• Profil terintegrasi

Di sini saya hanya ingin menunjukkan definisi intuitif dari integrasi, dan tidak melibatkan definisi simbol matematika yang ketat dan deduksi rumus yang ketat.

Jika Anda tertarik, lihat Wikipedia Cointegration. Kelas kuantitatif akan membahas hal-hal yang lebih mendalam di masa depan.

Mengapa harus merata/serasi?

Ini adalah salah satu dari beberapa hal yang dapat dilakukan untuk mencapai keselarasan.

Singkatnya, stabilitas adalah sifat dari suatu urutan yang tetap tidak berubah dari waktu ke waktu, dan ini adalah sifat yang sangat kita sukai ketika melakukan prediksi analisis data. Jika satu set data urutan waktu adalah stabil, itu berarti bahwa rata-rata dan diferensial tetap tidak berubah, sehingga kita dapat dengan mudah menggunakan beberapa teknik statistik pada urutan.

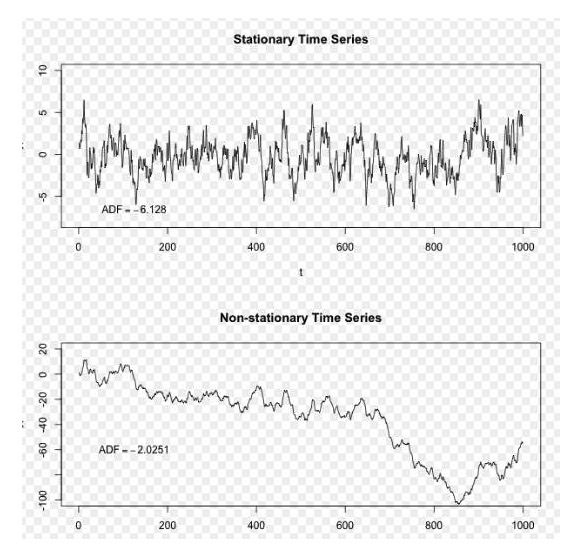
Gambar: Wikipedia

Dalam gambar di atas, urutan di atas adalah urutan yang stabil, dan kita dapat melihat bahwa ia selalu berfluktuasi di sekitar rata-rata jangka panjang, dan urutan di bawah adalah urutan yang tidak stabil, dan kita dapat melihat bahwa rata-rata jangka panjangnya berubah.

Sebagai contoh penerapan, jika urutan harga suatu aset (atau perbedaan harga dua urutan) adalah stabil, maka ketika ia menyimpang dari nilai rata-ratanya, orang dapat mengharapkan harga akan kembali ke nilai rata-ratanya pada suatu waktu di masa depan. Kita dapat memanfaatkan sifat ini untuk berinvestasi dan mendapatkan keuntungan. Misalkan nilai rata-rata jangka panjang suatu saham adalah 9, sedangkan nilai saat ini adalah 8. Jika setelah pemeriksaan, kita menganggap bahwa urutan historis saham ini memiliki sifat stabil, dan asumsi bahwa kesetaraan ini dapat dipertahankan, kita dapat membeli saham ini dan menunggu harganya kembali ke 9 di masa depan, sehingga mendapatkan keuntungan 1 dolar.

Ini adalah urutan harga saham yang stabil:

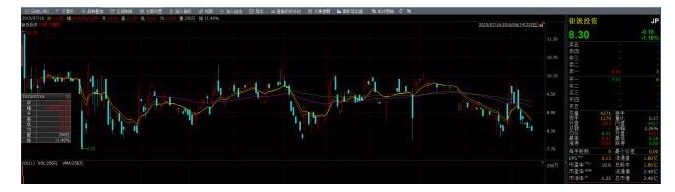
Stabilitas sangat berguna, tetapi dalam kenyataannya, sebagian besar saham tidak stabil, maka apakah kita masih dapat memanfaatkan sifat stabil untuk mendapatkan keuntungan? Jawabannya adalah ya, maka hubungan kointegrasi (cointegration) muncul! Jika dua kelompok urutan tidak stabil, tetapi kombinasi linier mereka dapat menghasilkan urutan yang stabil, maka kita mengatakan bahwa kedua kelompok data urutan waktu memiliki sifat kointegrasi, kita juga dapat menggunakan sifat statistik pada urutan dari kombinasi ini.

Sebagai contoh, jika perbedaan antara dua set data dalam urutan waktu adalah stabil, maka kita dapat melakukan investasi yang menguntungkan berdasarkan kesetimbangan perbedaan: ketika harga dua saham terlalu besar, berdasarkan kesetimbangan kita mengharapkan selisih harga akan menyusut, sehingga membeli saham dengan harga rendah, menjual saham dengan harga tinggi, dan menunggu harga kembali untuk melakukan operasi reversal sehingga menghasilkan keuntungan.

Ini adalah asal-usul pair trading.

• Stabilitas dan Metode Pemeriksaan

Strictly stationary dan weakly stationary (atau disebut covariance stationary, covariance stationary, dan lain-lain). Strictly stationary adalah suatu urutan yang selalu memiliki fungsi distribusi yang tidak berubah, sedangkan weakly stationary adalah suatu urutan yang memiliki konstanta deskriptif yang tidak berubah. Semua urutan yang kuat dan stabil memenuhi sifat weakly stationary, tetapi sebaliknya tidak berlaku.

Contoh aplikasi

Pertama-tama, perlu dicatat bahwa hubungan asosiasi bukanlah hubungan asosiasi. Kita secara artifisial membangun dua set data, sehingga secara intuitif melihat hubungan asosiasi. import numpy as np import pandas as pd import seaborn import statsmodels import matplotlib.pyplot as plt from statsmodels.tsa.stattools import coint

Konstruksi data

Pertama, kita membangun dua set data, masing-masing set data dengan panjang 100 . Set data pertama adalah 100 ditambah satu item tren ke bawah ditambah satu distribusi normal standar . Set data kedua berdasarkan data set pertama ditambah 30, ditambah satu distribusi normal standar tambahan .

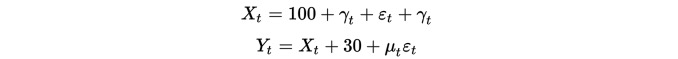
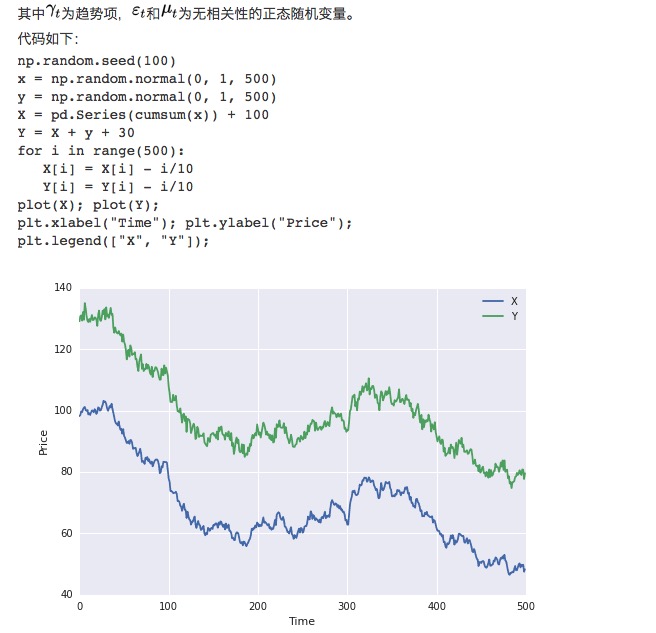
Jelas, kedua kelompok data ini tidak stabil, karena rata-rata berubah seiring berjalannya waktu. Namun kedua kelompok data ini memiliki hubungan integral, karena urutan diferensinya stabil:

plot(Y-X); plt.axhline((Y-X).mean(),color=“red”, linestyle=“–”); plt.xlabel(“Time”); plt.ylabel(“Price”); plt.legend([“Y-X”, “Mean”]);

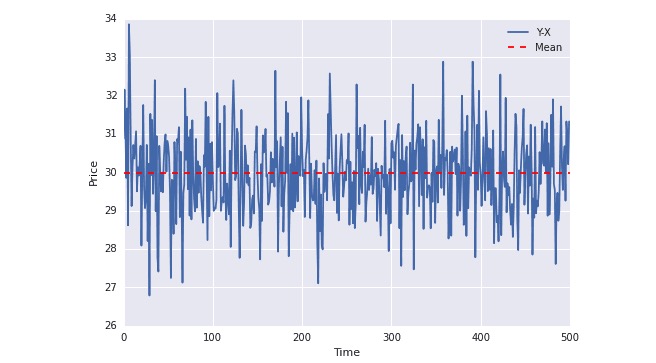
Dalam gambar di atas, dapat dilihat bahwa garis biru selalu berfluktuasi di sekitar nilai rata-rata. Nilai rata-rata tidak berubah seiring waktu (sebenarnya, hampir tidak berubah seiring waktu).

• Kesimpulan

Integrasi akan menjadi lebih rumit jika dibicarakan secara matematis, dan akan dibahas di kelas kuantitatif di masa depan. Kami hanya melakukan pengantar sederhana pada tingkat pengertian (level-0) untuk membuat Anda lebih memahami integrasi dengan aplikasi praktis.

Saya ingin berbagi dengan Anda, dari kelas kuantitatif ke kelas kuantitatif.