Ornstein-Uhlenbeck シミュレーションを Python で行う

本文では,オーンスタイン=ウレンベックプロセスを概要し,その数学式を記述し,それをPythonで実現し,シミュレートし,量化金融とシステム取引におけるいくつかの実用的な応用について議論します.また,より高度なランダムプロセスモデルであるオーンスタイン=ウレンベック (OU) プロセスを用いて,均等値回帰を表現する行動の時間配列をモデル化します.これは,デリバティブの価格設定における利息モデリングおよび取引時にアルゴリズムを実行するシステム取引に特に有用です.

オーンシュタイン・ウレンベックプロセスは?

オーンスタイン=ウレンベックプロセスは,均等値回帰の振る舞いをモデリングするために使用される連続時間ランダムプロセスの1つです.これは,無限に漂流できる標準的なランダムな移動やブラウンの運動とは異なり,OUプロセスは時間の経過とともに長期平均値に戻ることが多いことを意味します.数学的に言えば,OUプロセスは,このような均等値回帰の振る舞いを制御する特定のランダム微分方程式 (SDE) の解です.OUプロセスのSDEは,次の式によって与えられます:

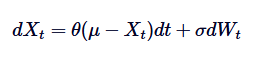
Xt は,時間 t のランダムな過程を表し,μ は長期平均値,θ は平均回帰率,δ は波動性,dWt は Wiener プロセスまたは標準ブラウン運動である.

歴史的背景と応用

オルンスタイン=ウレンベックプロセスは,最初にレオナルド・オルンスタインとジョージ・ユージーン・ウレンベックによって1930年に提案され,摩擦状態下でブラウン運動を行う粒子の速度を模擬するために使用された.時間とともに,その実用性は物理を超えて,生物学,化学,経済学,金融学など様々な分野に適用されるようになった.

定量金融では,OUプロセスは平均回帰の振る舞いを示す現象をモデル化するのに特に有用である. 有名な例には,金利,為替レート,金融市場の変動などがある. 例えば,人気の金利モデルであるVasicekモデルは,OUプロセスから直接導かれる.

量的な金融における重要性

オーンスタイン=ウレンベックプロセスは,量化金融において重要な理由である.その平均値回帰の性質は,金融変数をモデル化するために自然に選択されるものとする.これらの金融変数は,ランダムな流動ではなく,安定した長期平均値の波動を表現する.この性質は,平均値回帰が中央銀行による長期安定の利率への影響を反映する金利モデル化において重要である.

さらに,OUプロセスは,資産価格モデル (衍生品の評価を含む) とリスク管理戦略に使用される.また,Cox-Ingersoll-Ross (CIR) モデルのようなより複雑なモデルの構成要素として使用され,OUプロセスは非負の利率をモデル化する拡張モデルとなる.

主要な特徴と直感

オルンスタイン・ウレンベックプロセスの主な特徴は以下の通りである.

• 平均値回帰:OUプロセスは,長期平均値μに戻る傾向がある.これは,ブラウンの運動などのプロセスとは顕著に対照的に,後者はそのような傾向を示していない.
• 波動性:パラメータδは,制御プロセスにおけるランダム性または変動性のレベルである.波動性が高いほど,プロセスが回帰前の平均値からの偏差が大きい.
• 戻る速度:参数θは,プロセスの平均回帰速度を決定する.θ値は高くなるほど,平均回帰速度は速い.
• 安定性:OUプロセスは平坦である,つまりその統計的特性は時間とともに変化しない.これは金融界の安定システムモデリングに不可欠である.

直感的に,あなたはオーンスタイン-ウレンベック過程を平均値の周りに伸びる皮筋の行動をモデル化すると考えることができる.この過程は,ランダムな波動によって均等値から逸脱する可能性があるが,皮筋の拉力 (均等値回帰に似た) は,それが最終的に均等値に戻ることを保証する.

他のランダムプロセスと比較する

OUプロセスは様々な金融現象のモデリングと密接に関連しているため,他のランダムなプロセス (例えば,ブラウンの運動と幾何的なブラウンの運動 (GBM)) とよく比較される.ブラウンの運動とは異なり (ブラウンの運動には均等な回帰の傾向がない),OUプロセスは明らかな均等な回帰の振る舞いを有する.これは,変数が安定した均衡の周りに波動するシナリオをモデリングするのに適している.

OUプロセスは,通常株式価格をモデリングするために使用され,漂流と波動項目を含むGBMと比較して,指数的な成長を示さないが,その平均値の振動を中心に示している.GBMは時間とともに増加する数量についてモデル化するのに適しており,OUプロセスは平均値回帰特性を示す変数についてモデル化するのに最適である.

量的な金融の例

オーンスタイン=ウレンベックプロセスは金融分野において,特に平均値回帰が重要な特徴であるモデリングシナリオにおいて,広範な応用があります.以下では,最も一般的な使用例について説明します.

利子率モデリング

OUプロセスの最も顕著な応用の一つは,特にワシシェクモデルの枠組みの中で利率をモデリングすることである.ワシシェクモデルは利率がOUプロセスに従っていることを仮定し,利率は時間の経過とともに長期平均値に戻る傾向がある.この特徴は,利率がしばしば無限に変動せず,経済条件によって影響される平均値の近くで波動するので,正確な模擬利率行動に不可欠である.

資産価格

OUプロセスは,資産の価格設定において,特に固定収益証券において,通常,債券の収益率の進化を模擬するために用いられる.OUプロセスの平均回帰性性質は,収益率が歴史的平均値から遠く離れないことを保証し,これは観察された市場行動と一致する.OUプロセスは,債券や他の利率敏感なツールの価格設定に貴重なツールとなる.

配合取引戦略

配合取引は,市場中立的な戦略であり,関連する2つの資産で負債を確立する.この場合,OUプロセスは特に有用であり,両資産間の価格差をモデル化することができ,価格差は通常均等値回帰である.OUプロセスの価格差をモデル化することで,トレーダーは価格差が平均値から逸脱する際に利益の入口と出口点を確認し,回帰均等値を予測し,取引信号を生成することができる.

例えば,2つのフューチャー間の差値がある値を超えると,トレーダーは優れたパフォーマンスのフューチャーと多くの不良パフォーマンスのフューチャーを空売りし,差値が歴史的な平均値に戻ることを期待し,逆転が起きた場合,利益を得ることができる.

オーンスタイン=ウレンベック SDEの解答

Ornstein-Uhlenbeck プロセスの微分方程式式は,その解の基礎である. この SDE を解くために,積因数法を使います. SDE を書き換えましょう:

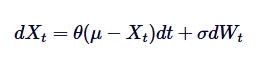
この2つの項を足し算します. :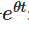

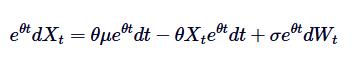
この2つの辺を足すと,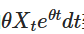余剰分は,x=1で,x=2で,x=2で,x=2で,x=2で,x=2で,x=2で,x=2で,x=2で,x=2で,x=2で,x=2で,x=2で,x=2で,y=2で,y=2で,y=2で,y=2で,y=2で,y=2で,y=2で,y=2で,y=2で,y=2で,y=2で,y=2で,y=2で,y=2で,y=2で,y=2で,y=2で,y=2で,y=2で,y=2で,y=2で,y=2で,y=2で,y=2で,y=2で,y=2で,y=2で,y=2で,y=2で,y=2で,y=2で,y=2で,y=2で,y=2で,y=2で,y=2で

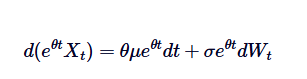
この2つの辺を0からtに積むと,

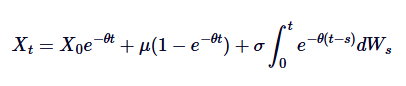
これはオーンスタイン=ウレンベックSDEの一般解である.

明らかに解決法にはいくつかの重要な意味があります.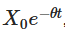初期値が時間の経過とともに衰退し,その過程がどのように徐々に始まりを忘れていくかを示します.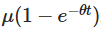プロセスが時間とともに平均値μに傾いていることを表す.第三項はランダム性を導入し,ウィーナープロセスに関する積分がランダム波動を説明する.

このソリューションは,定性均等値回帰行動とブラウンの運動によって駆動されるランダム分数のバランスを強調する.このソリューションを理解することは,OUプロセスを効果的に模擬するために重要であり,以下のように説明される.

他のランダムなプロセスとの関連

オーンスタイン=ウレンベックプロセスは,他の有名なランダムプロセス (ブラウンの運動やワシシェックモデルを含む) といくつかの重要な関連性がある.

ブラウン運動との関係

オーンシュタイン=ウレンベックプロセスは,ブラウンの運動の均等回帰のバージョンと考えられる.ブラウンの運動は,独立増量で均等回帰のない傾向を記述するプロセスであり,OUプロセスは,漂流項を使用してブラウンの運動を修正して平均回帰を導入し,それによってプロセスを中心値に引き戻す.数学的に,もしθ=0を設定すると,OUプロセスは波動を持つ標準的なブラウンの運動に簡素化される:

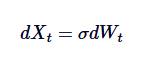
したがって,ブラウンの運動は,平均回帰の欠如に対応するOUプロセスの例外である.

ワシシェクモデルとの関係

ヴァシシェックモデルは,利率モデリングに広く使われており,本質的にはオーンスタイン=ウレンベック過程の利率進化における応用である.ヴァシシェックモデルは,利率がOU過程に従っていると仮定し,SDEは以下のように定義される.

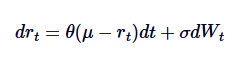
その中,rtは短期金利を表し,参数θ,μ,δの解釈は,OUの過程における解釈と類似している.ワシシェックモデルは,平均値回帰金利経路を生成できる.これは金融モデリングにおける主な利点の1つです.

これらの関係を理解することで,様々な環境,特に金融分野におけるOUプロセスの使用方法についてより広く理解することができます.この関連性の実用的な意味については,以下の応用例について説明します.

Ornstein-Uhlenbeck プロセスを Python で模倣する

このセクションでは,PythonでOrnstein-Uhlenbeck (OU) プロセスを模倣する方法について説明します.これは,OUプロセスを定義するランダム微分方程式 (SDE) をEuler-Maruyama離散を用いて離散することを意味します.

SDEの分散

SDEの数学式を振り返って,それぞれの項目を概要してみましょう.

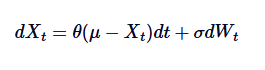
その中で,

• Xt は,プロセスが時間 t のときの値である.
• 平均回帰速度が θ である.
• プロセスの長期平均値である.
• δは波動率パラメータである.
• dWtはウィーナープロセス (標準ブラウン運動) の増量を表します.

このプロセスをコンピュータでシミュレートするには,連続時間SDEを分散する必要があります.一般的な方法の一つは,小さな分散時間のステップを考慮して長さを考えるEuler-Maruyama分散です.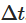近い連続プロセスである.オーンスタイン-ウレンベックプロセスの離散形態は,以下のように表される.

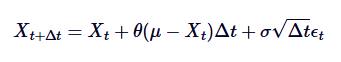
その中で,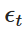標準正規分布から抽出されたランダムな変数である.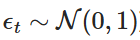) ;この分散化により,時間とともにXtの値を反復計算し,OUプロセスの動作を模倣することができる.

Pythonの実装

この例では,Pythonの NumPy と Matplotlib のみを使用します.

まず,標準的な方法で NumPy と Matplotlib を輸入します.次に,OU モデルにすべての参数を指定します.次に,N の長さの NumPy 配列を事前に割り当て,OU 経路を計算した後にそれに追加します.それから,N-1 ステップを繰り返します (ステップ 1 は指定された初期条件 X0 です),dW を模倣してランダム増量します.そして,上記の数学式に基づいて OU 経路の次の代数を計算します.最後に,Matplotlib を使用して経路の歴史を描きます.

import numpy as np
import matplotlib.pyplot as plt

# Parameters for the OU process
theta = 0.7      # Speed of mean reversion
mu = 0.0         # Long-term mean
sigma = 0.3      # Volatility
X0 = 1.0         # Initial value
T = 10.0         # Total time
dt = 0.01        # Time step
N = int(T / dt)  # Number of time steps

# Pre-allocate array for efficiency
X = np.zeros(N)
X[0] = X0

# Generate the OU process
for t in range(1, N):
    dW = np.sqrt(dt) * np.random.normal(0, 1)
    X[t] = X[t-1] + theta * (mu - X[t-1]) * dt + sigma * dW

# Plot the result
plt.plot(np.linspace(0, T, N), X)
plt.title("Ornstein-Uhlenbeck Process Simulation")
plt.xlabel("Time")
plt.ylabel("X(t)")
plt.show()

グラフの結果は以下の通りです.

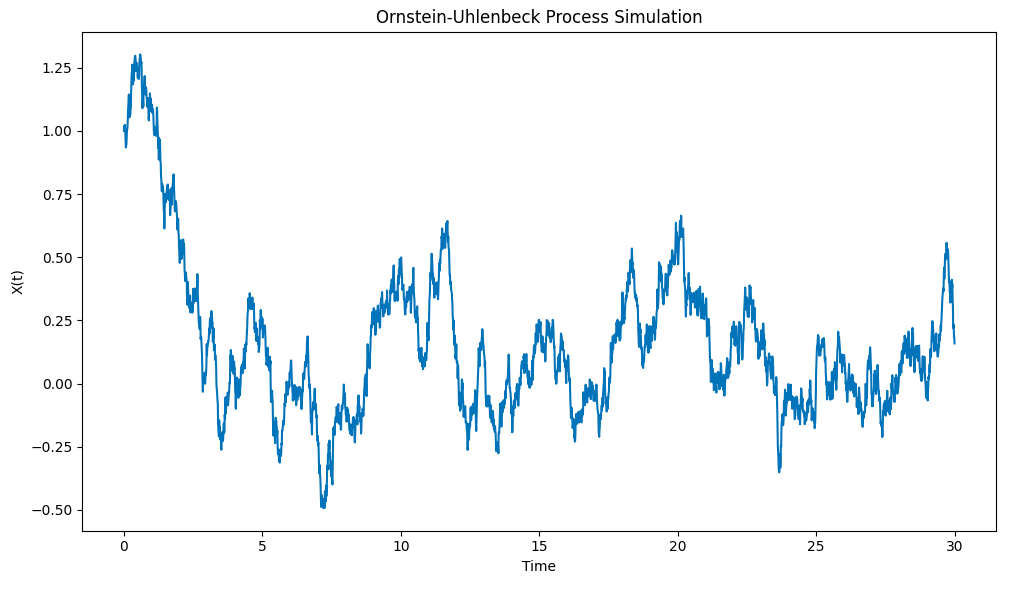
Python で描いたオーンスタイン=ウレンベックプロセスシミュレーション

このプロセスは,どのように初期条件から,素早くをX0=1から平均値μ=0に引っ張って,その平均値から逸脱すると,その平均値に戻る傾向を示すか見てみましょう.

概要と次のステップ

この記事では,オーンスタイン-ウレンベックプロセスを概要し,その数学式を説明し,連続時間のSDEの離散バージョンを模擬するための基本的なPythonの実装を提供します. 次の記事では,OUプロセスをベースに構築されたより複雑なSDEを研究し,それらをシステム取引および衍生品価格設定アプリケーションで使用する方法について学びます.

完全なコード

# OU process simulation

import numpy as np
import matplotlib.pyplot as plt

# Parameters for the OU process
theta = 0.7      # Speed of mean reversion
mu = 0.0         # Long-term mean
sigma = 0.3      # Volatility
X0 = 1.0         # Initial value
T = 30.0         # Total time
dt = 0.01        # Time step
N = int(T / dt)  # Number of time steps

# Pre-allocate array for efficiency
X = np.zeros(N)
X[0] = X0

# Generate the OU process
for t in range(1, N):
    dW = np.sqrt(dt) * np.random.normal(0, 1)
    X[t] = X[t-1] + theta * (mu - X[t-1]) * dt + sigma * dW

# Plot the result
plt.plot(np.linspace(0, T, N), X)
plt.title("Ornstein-Uhlenbeck Process Simulation")
plt.xlabel("Time")
plt.ylabel("X(t)")
plt.show()

ブログの記事へのリンク:https://www.quantstart.com/articles/ornstein-uhlenbeck-simulation-with-python/

もっと