몰코프 모형

몰코프 모형

• 1. 아는 것

  오늘 우리는 HMM (인마르코프 모델) 의 간단한 적용을 주식에 대해 소개합니다.

  마르코프 모형은 초라하게 들릴 수도 있고, 어떤 모형인지 전혀 알 수 없을 수도 있습니다. 그럼 한 걸음 물러서서 마르코프 체인 (Markov Chain) 을 먼저 살펴보겠습니다.

  마르코프 연쇄 (Markov Chain), 안드레 마르코프 (A.A. 마르코프, 1856-1922) 의 이름을 따서 붙여진 (아래의 이 사람) 은 수학에서 마르코프 특성을 가진 분산 사건의 무작위 과정을 의미한다. 현재 지식이나 정보를 제공한 상태에서 과거 (즉 현재 전의 역사적 상태) 는 예측 가능한 미래 (즉 현재 이후의 미래 상태) 에 무관하다.

  

  이 과정에서는 각 상태의 전환이 이전 n 상태에만 의존하고 있으며, 이 과정은 n 단계의 1 모델로 불리며, 여기서 n는 전환 상태에 영향을 미치는 상태의 수이다. 가장 간단한 마르코프 과정은 1 단계 과정이며, 각 상태의 전환은 이전 상태에만 의존한다.

• 두 번째 예제

  수학적인 표현으로 표현하면 다음과 같습니다.

  

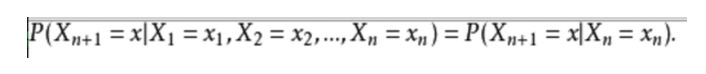
  일상의 예를 들어서, 우리는 현재 날씨 상황에 따라 미래의 날씨를 예측하고자 합니다. 한 가지 방법은 이 모델의 각 상태가 이전 상태에만 의존한다는 가정, 즉 마르코프의 가정, 이 가정은 문제를 크게 단순화 할 수 있습니다. 물론, 이 예제도 다소 비현실적입니다. 그러나, 이러한 단순화된 시스템이 우리의 분석에 유리할 수 있으므로, 우리는 일반적으로 이러한 가정을 받아들이고 있습니다. 왜냐하면 우리는 그러한 시스템이 우리에게 유용한 정보를 얻을 수 있다는 것을 알고 있기 때문입니다.

  

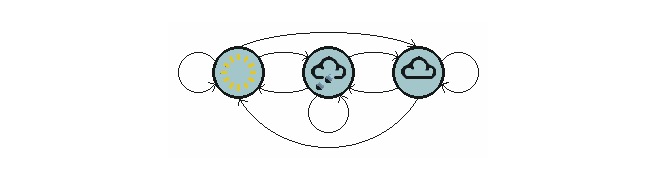
  위 그림은 날씨가 이동하는 모델을 보여줍니다.

  N 상태가 있는 1단계 과정에는 N2개의 상태 전환이 있다. 각각의 전환의 확률은 상태 전환 확률, 즉 한 상태에서 다른 상태로 이동하는 확률이다. 이 모든 N2의 확률은 상태 전환 매트릭스로 나타낼 수 있으며, 위의 날씨 예의 상태 전환 매트릭스는 다음과 같다.

  

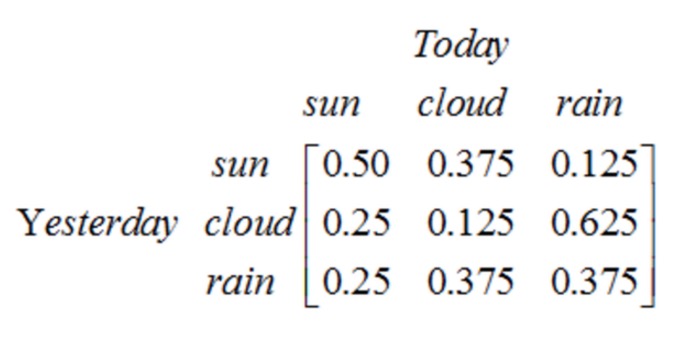
  이 매트릭스는 어제 날씨가 흐르면 25%가 날씨가 좋아질 확률이 12.5%가 흐르면 62.5%가 비가 올 확률이 있고 매트릭스의 각 행의 합이 1이 되는 것을 의미합니다.

  이런 시스템을 초기화하려면 초기 확률 벡터가 필요합니다.

  

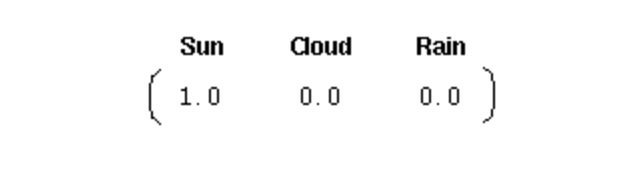
  이 벡터는 첫날이 맑을 것을 나타냅니다. 여기까지 우리는 위의 1단계 마르코프 과정에 대해 다음 세 부분을 정의했습니다.

  상태: 맑은 날씨, 흐린 날씨, 비가 올린다.

  초기 벡터: 시간 0에서 시스템의 상태를 정의하는 확률.

  상태 전환 매트릭스: 모든 기상 변환의 확률. 이렇게 설명할 수 있는 모든 시스템은 마르코프 과정이다.

  그러나, 마르코프 과정이 충분히 강력하지 않을 때 우리는 어떻게 해야 할까요? 어떤 경우에는 마르코프 과정이 우리가 발견하기를 희망하는 패턴을 설명하기에 충분하지 않습니다.

  예를 들어 우리의 주식 시장은, 만약 단지 시장을 관찰하는 것이라면, 우리는 당일의 가격, 거래량 등 정보만을 알 수 있지만, 현재 주식 시장이 어떤 상태에 있는지 알 수 없습니다. 이 경우 우리는 두 개의 상태 집합, 관찰 가능한 상태 집합 (주식 시장 가격 거래 상태 등) 과 숨겨진 상태 집합 (주식 시장 상태) 을 가지고 있습니다. 우리는 주식 시장의 거래량과 마르코프 가설에 따라 주식 시장의 상태를 예측할 수 있는 알고리즘을 찾을 수 있기를 바랍니다.

  위와 같은 경우, 관찰 가능한 상태의 연속과 숨겨진 상태의 연속은 확률과 관련이 있다. 따라서 우리는 이러한 유형의 과정을 숨겨진 마르코프 과정과 이 숨겨진 마르코프 과정의 확률과 관련이 있고 관찰 가능한 상태의 집합, 즉 숨겨진 마르코프 모델로 모델링할 수 있다.

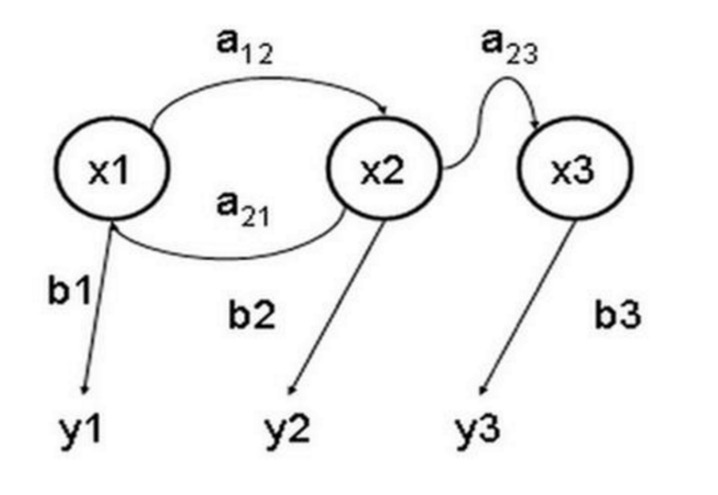
  숨겨진 마르코프 모델 (Hidden Markov Model) 은 암묵적인 알 수 없는 매개 변수를 포함하는 마르코프 프로세스를 설명하는 통계 모델이다. 어려운 점은 관찰 가능한 매개 변수로부터 프로세스의 암묵적 매개 변수를 결정하고 그 매개 변수들을 사용하여 추가 분석을 하는 것이다. 아래 그림은 3개의 상태의 숨겨진 마르코프 모델의 상태 변환 그래프이다. x는 암묵적인 상태를 나타내고, y는 관찰 가능한 출력을 나타내고, a는 상태 변환 확률을 나타내고, b는 출력 확률을 나타낸다.

  

  의 예로 설명하자면: 내 손에 세 개의 다른 이 있다고 가정하자. 첫 번째 은 우리가 흔히 사용하는 입니다. 이 을 D6라고 부릅니다. 6개의 면이 있고, 각 면이 1,2,3,4,5,6의 확률이 1/6입니다. 두 번째 은 사각형입니다. 이 을 D4라고 부릅니다. 각 면은 1,2,3,4의 확률이 1/4입니다. 세 번째 은 8개의 면이 있습니다. 이 을 D8이라고 부릅니다. 각 면은 1,2,3,4,5,6,7,8의 확률이 1/8입니다.

  

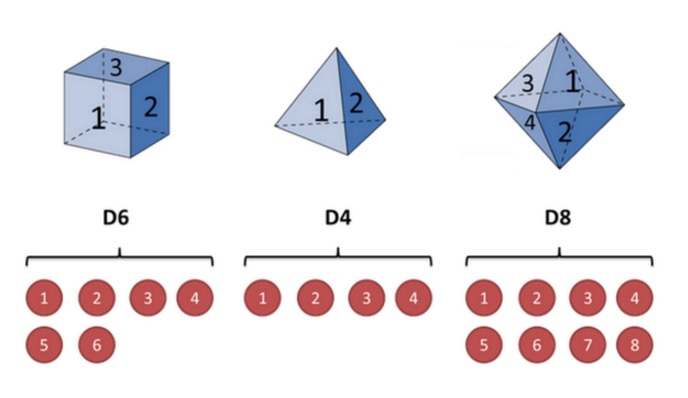
  만약 우리가 주사위를 시작한다면, 먼저 3개의 주사위 중 하나를 선택하고, 각각의 주사위를 뽑는 확률은 1/3이다. 그리고 주사위를 치면, 숫자가 1,2,3,4,5,6,7,8 중 하나를 얻습니다. 계속 반복하면, 각 숫자가 1,2,3,4,5,6,7,8 중 하나를 얻습니다. 예를 들어, 우리는 이런 숫자를 얻을 수 있습니다.

  이 숫자의 행렬은 보이는 상태의 행렬이라 불립니다. 하지만 몰코프 모형에서는 보이는 상태의 행렬뿐만 아니라 암시된 상태의 행렬도 있습니다. 이 예에서 암시된 상태의 행렬은 여러분이 사용하는 주머니의 행렬입니다. 예를 들어, 암시된 상태의 행렬은 D4 D6 D8 D6 D4 D8 D6 D6 D6 D4 될 수 있습니다.

  一般来说，HMM中说到的马尔可夫链其实是指隐含状态链，因为隐含状态（骰子）之间存在转换概率。在我们这个例子里，D6的下一个状态是D4，D6，D8的概率都是1/3。D4，D8的下一个状态是D4，D6，D8的转换概率也都一样是1/3。这样设定是为了最开始容易说清楚，但是我们其实是可以随意设定转换概率的。比如，我们可以这样定义，D6后面不能接D4，D6后面是D6的概率是0.9，是D8的概率是0.1。这样就是一个新的HMM。

  마찬가지로, 가시 상태 사이에는 변환 확률이 없지만, 함축 상태와 가시 상태 사이에는 출력 확률이라고 불리는 확률이 있습니다. 우리 예제에서, 6면 주머니 (D6) 의 출력 확률은 1/6입니다. 2,3,4,5,6의 출력 확률은 1/6입니다. 우리는 또한 출력 확률에 대해 다른 정의를 할 수 있습니다. 예를 들어, 내가 카지노에서 움직인 6면 주머니를 가지고 있는데, 출력 확률은 1보다 크며 1/2이고, 출력 확률은 2,3,4,5,6입니다.

  

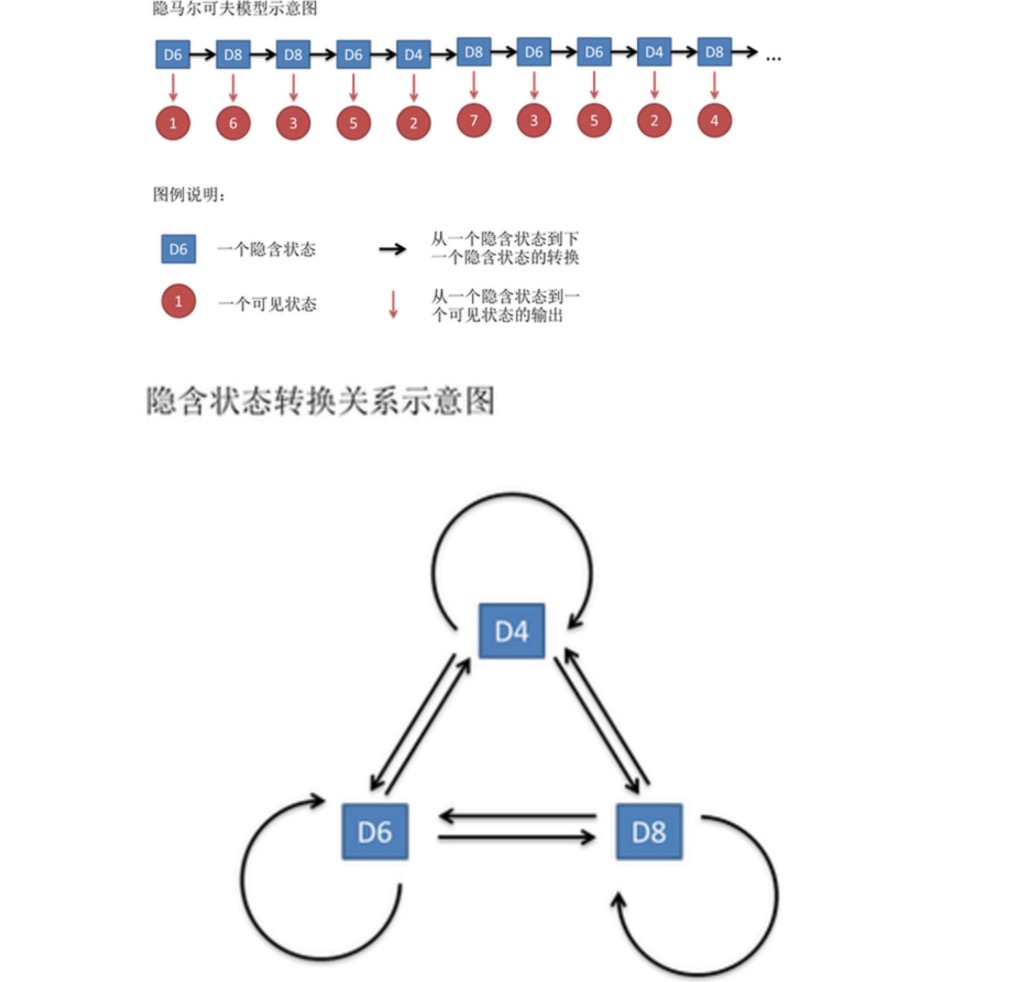
  사실 HMM의 경우, 모든 암묵 상태 사이의 변환 확률과 모든 암묵 상태에서 모든 가시 상태 사이의 출력 확률을 미리 알고 있다면, 모형을 만드는 것이 상당히 쉽습니다. 그러나 HMM 모델을 적용할 때, 종종 일부 정보가 부족합니다. 때때로 당신은 몇 가지 이 있고, 각 이 무엇인지 알고 있지만, 의 순서를 알지 못합니다. 때로는 당신은 단지 많은 의 결과를보고, 나머지는 아무것도 모릅니다. 알고리즘을 적용하면 이러한 잃어버린 정보를 추정하는 것이 중요한 문제입니다.

  HMM 모델과 관련된 알고리즘은 크게 세 가지로 분류되며 세 가지 문제를 해결합니다.

  • 몇 개의 이 있는지 알고 있습니다 (임의 상태 수), 각각의 이 무엇인지 알고 있습니다 (변환 확률), 이 하는 결과에 따라 (시각 상태 체인), 나는 이 때마다 어떤 이 있는지 알고 싶습니다 (임의 상태 체인).

  • 또한 몇 개의 이 있는지 알고 있습니다 (임의 상태 수), 각각의 이 무엇인지 알고 있습니다 (변환 확률), 이 던지는 결과에 따라 (보기 상태 사슬) 나는 이 결과를 던지는 확률을 알고 싶습니다.

  • 몇 개의 이 있다는 것을 알고 (임의상 상태의 수), 각각의 이 무엇인지 모르고 (변환 확률), 많은 의 결과를 관찰하고 (보인 상태의 연쇄), 각각의 이 무엇인지 반발하고 싶습니다 (변환 확률).

    만약 상위 주식시장의 문제를 해결하려면 문제 1과 문제를 해결해야 합니다. 다음 기사에서는 어떻게 하는지 살펴볼 것입니다.

이 부분의 본문은 http://www.moneycode.com/