Model Markov yang tersembunyi

Model Markov yang tersembunyi

• Pertama, mengenali

  Hari ini kita akan membentangkan aplikasi mudah HMM (model Inmarkov) pada saham.

  Model Markov yang tersembunyi, yang pada mulanya terdengar tinggi, tidak tahu apa sebenarnya, jadi mari kita ambil langkah ke belakang dan lihat rantai Markov terlebih dahulu.

  Rantai Markov, dinamakan selepas Andrey Markov (A.A. Markov, 1856-1922), ialah proses rawak peristiwa yang mempunyai sifat Markov dalam matematik. Dalam keadaan pengetahuan atau maklumat semasa, masa lalu (iaitu keadaan sejarah sebelum masa kini) tidak relevan untuk meramalkan masa depan (iaitu keadaan masa depan selepas masa kini).

  

  Dalam proses ini, perpindahan setiap keadaan hanya bergantung kepada n keadaan sebelumnya, proses ini dikenali sebagai model satu peringkat n, di mana n adalah bilangan keadaan yang mempengaruhi perpindahan. Proses Markov yang paling mudah adalah proses peringkat satu, perpindahan setiap keadaan hanya bergantung kepada keadaan sebelumnya.

• Contoh kedua

  Perkataan matematiknya adalah seperti berikut:

  

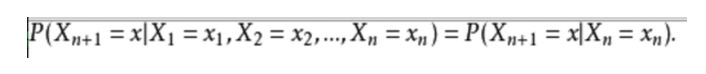
  Untuk memberikan contoh kehidupan seharian, kita ingin meramalkan keadaan cuaca masa depan berdasarkan keadaan cuaca semasa. Salah satu cara adalah dengan mengandaikan bahawa setiap keadaan dalam model ini hanya bergantung kepada keadaan sebelumnya, iaitu hipotesis Markov, hipotesis yang sangat memudahkan masalah ini. Sudah tentu, contoh ini juga agak tidak praktikal.

  

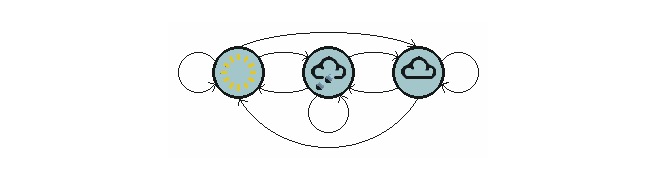
  Gambar di atas menunjukkan model perubahan cuaca.

  Perhatikan bahawa proses tahap pertama yang mengandungi N keadaan mempunyai N2 perpindahan keadaan. Kebarangkalian setiap perpindahan dipanggil kebarangkalian perpindahan keadaan, iaitu kebarangkalian perpindahan dari satu keadaan ke keadaan lain. Semua kebarangkalian N2 ini boleh dinyatakan dengan matriks perpindahan keadaan, seperti dalam contoh cuaca di atas:

  

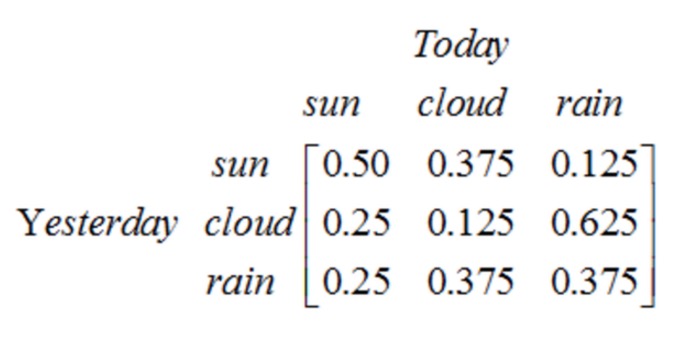
  Matriks ini menyatakan bahawa jika hari kemaren hari mendung, maka 25% kemungkinan hari ini adalah hari yang cerah, 12.5% kemungkinan hari mendung, 62.5% kemungkinan hujan, dan jelas, setiap baris dalam matriks adalah 1.

  Untuk memulakan sistem seperti ini, kita memerlukan vektor kebarangkalian awal:

  

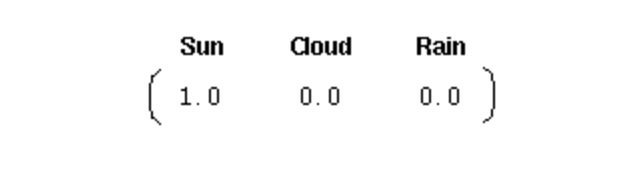
  Vektor ini menunjukkan bahawa hari pertama adalah hari yang cerah. Di sini, kita telah menentukan tiga bahagian untuk proses Markov tahap pertama di atas:

  Status: Hari cerah, mendung dan hujan.

  Vektor awal: Menentukan kebarangkalian keadaan sistem pada waktu 0.

  Matriks perpindahan keadaan: kebarangkalian setiap perubahan cuaca. Semua sistem yang boleh digambarkan seperti ini adalah proses Markov.

  Walau bagaimanapun, apa yang perlu kita lakukan apabila proses Markov tidak cukup kuat? Dalam beberapa kes, proses Markov tidak cukup untuk menggambarkan corak yang kita ingin temui.

  Sebagai contoh, jika kita hanya melihat pasaran saham, kita hanya dapat mengetahui harga, jumlah dagangan dan lain-lain pada hari itu, tetapi tidak tahu apa keadaan pasaran saham semasa (bull market, bear market, shocks, rebound, dan lain-lain), dalam kes ini kita mempunyai dua set keadaan, satu set keadaan yang dapat dilihat (stock market price trading status dan lain-lain) dan satu set keadaan tersembunyi (stock market status); kita berharap dapat mencari algoritma yang boleh meramalkan keadaan pasaran saham berdasarkan keadaan harga saham dan hipotesis Markov.

  Dalam kes-kes di atas, urutan keadaan yang boleh diperhatikan dan urutan keadaan yang tersembunyi adalah berkaitan dengan kebarangkalian. Oleh itu, kita boleh memodelkan proses jenis ini sebagai satu proses Markov tersembunyi dan satu set keadaan yang berkaitan dengan kebarangkalian proses Markov tersembunyi dan dapat diperhatikan, iaitu model Markov tersembunyi.

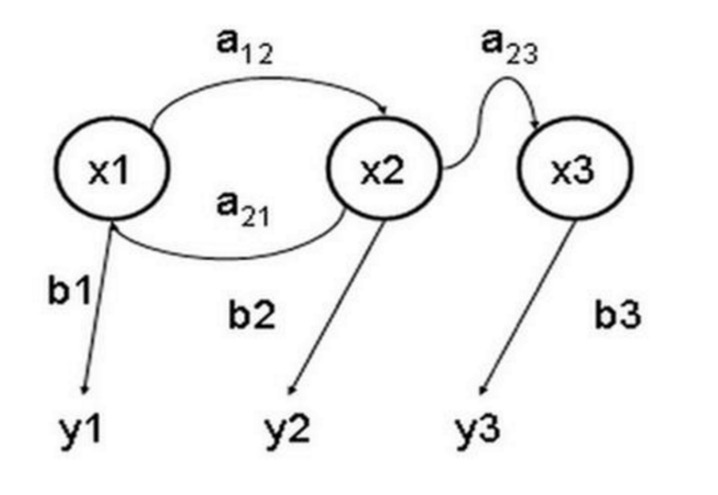
  Model Markov yang tersembunyi adalah model statistik yang digunakan untuk menggambarkan proses Markov yang mengandungi parameter yang tidak diketahui secara tersirat. Masalahnya adalah untuk menentukan parameter tersirat proses dari parameter yang dapat dilihat dan kemudian menggunakan parameter tersebut untuk analisis lanjut. Gambar berikut adalah peta pemindahan keadaan model Markov tiga keadaan, di mana x mewakili keadaan tersirat, y mewakili output yang dapat dilihat, a menunjukkan kemungkinan penukaran keadaan, dan b menunjukkan kemungkinan output.

  

  Sebagai contoh, katakan saya mempunyai tiga ekor ekor yang berbeza di tangan saya; ekor pertama adalah ekor biasa kami (menamakan ekor ini D6), dengan 6 muka, dan setiap muka (menentukan 1, 2, 3, 4, 5, 6) mempunyai kebarangkalian 1/6. Ekor kedua adalah ekor empat (menentukan D4), dan setiap muka (menentukan 1, 2, 3, 4) mempunyai kebarangkalian 1/4. Ekor ketiga mempunyai lapan muka (menentukan D8), dan setiap muka (menentukan 1, 2, 3, 4, 5, 6, 7, 8) mempunyai kebarangkalian 1/8.

  

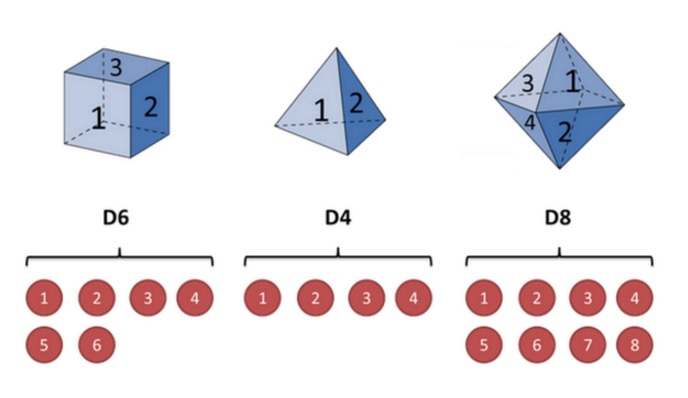
  Katakan kita mulakan dengan dadu, kita mulakan dengan memilih satu daripada tiga dadu, dan peluang untuk memilih setiap dadu adalah 1/3. Kemudian kita pilih dadu, mendapat nombor, 1, 2, 3, 4, 5, 6, 7, 8. Ulangi proses ini terus-menerus, kita akan mendapat satu siri nombor, setiap nombor adalah 1, 2, 3, 4, 5, 6, 7, 8.

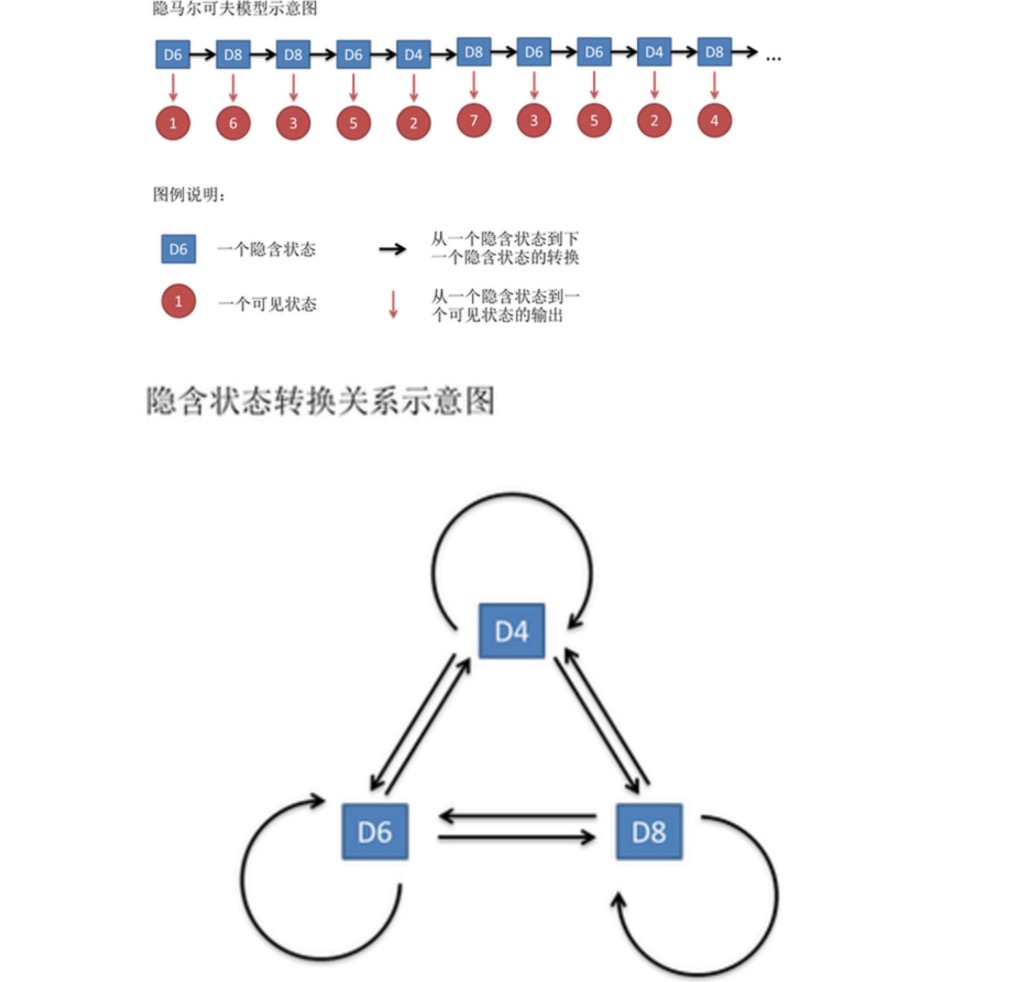
  Barisan ini dipanggil rantai keadaan yang kelihatan. Tetapi dalam model Markov tersembunyi, kita mempunyai bukan hanya rantai keadaan yang kelihatan, tetapi juga rantai keadaan yang tersirat. Dalam contoh ini, rantai keadaan tersirat adalah urutan rak yang anda gunakan. Sebagai contoh, rantai keadaan tersirat mungkin: D4 D6 D8 D6 D4 D8 D6 D6 D6 D4.

  一般来说，HMM中说到的马尔可夫链其实是指隐含状态链，因为隐含状态（骰子）之间存在转换概率。在我们这个例子里，D6的下一个状态是D4，D6，D8的概率都是1/3。D4，D8的下一个状态是D4，D6，D8的转换概率也都一样是1/3。这样设定是为了最开始容易说清楚，但是我们其实是可以随意设定转换概率的。比如，我们可以这样定义，D6后面不能接D4，D6后面是D6的概率是0.9，是D8的概率是0.1。这样就是一个新的HMM。

  Begitu juga, walaupun tidak ada kebarangkalian penukaran antara keadaan yang kelihatan, terdapat kebarangkalian antara keadaan tersirat dan keadaan yang kelihatan yang dipanggil kebarangkalian output. Dalam contoh kita, kebarangkalian output 1 dari dadu enam sisi (D6) adalah 1/6. Kebarangkalian menghasilkan 2, 3, 4, 5, 6 juga 1/6. Kita juga boleh membuat definisi lain mengenai kebarangkalian output.

  

  Sebenarnya untuk HMM, simulasi adalah agak mudah jika anda mengetahui terlebih dahulu kebarangkalian penukaran antara semua keadaan tersirat dan kebarangkalian output antara semua keadaan tersirat ke semua keadaan yang dapat dilihat. Tetapi apabila menggunakan model HMM, selalunya ada sebahagian maklumat yang hilang, kadang-kadang anda tahu beberapa jenis boneka, apa setiap boneka, tetapi tidak tahu urutan boneka yang keluar; kadang-kadang anda hanya melihat hasil banyak boneka, dan tidak tahu apa-apa yang tersisa.

  Algoritma yang berkaitan dengan model HMM terbahagi kepada tiga kategori utama, masing-masing menyelesaikan tiga masalah:

  • Mengetahui bahawa terdapat beberapa jenis monkey (jumlah keadaan tersirat), apa setiap jenis monkey (kemungkinan penukaran), dan berdasarkan hasil monkey (rantai keadaan yang dapat dilihat), saya ingin tahu apa jenis monkey (rantai keadaan tersirat) yang keluar setiap kali.

  • Saya ingin tahu berapa banyak (jumlah keadaan tersirat) dan apa (kemungkinan penukaran) setiap (kemungkinan penukaran), dan berdasarkan hasil penukaran (rantai keadaan yang kelihatan), saya ingin tahu kemungkinan penukaran ini.

  • Mengetahui bahawa terdapat beberapa jenis monyet (jumlah keadaan tersirat), tidak tahu apa setiap jenis monyet (kemungkinan penukaran), mengamati banyak hasil monyet (rantai keadaan yang kelihatan), saya ingin membalikkan apa setiap jenis monyet (kemungkinan penukaran).

    Jika kita mahu menyelesaikan masalah di pasaran saham di atas, kita perlu menyelesaikan masalah 1 dan 3.

Dibaharui dari: