Simulação Ornstein-Uhlenbeck com Python

Neste artigo, descreveremos o processo Ornstein-Uhlenbeck, descrevemos sua fórmula matemática, implementamos e simulamos com Python, e discutimos algumas aplicações práticas na quantificação financeira e no comércio sistêmico. Usaremos um modelo de processo aleatório mais avançado, chamado processo Ornstein-Uhlenbeck (OU), que pode ser usado para modelar sequências de tempo que representam ações de regressão de igual valor.

O que é o processo Ornstein-Uhlenbeck?

O processo de Ornstein-Uhlenbeck é um processo aleatório em tempo contínuo usado para modelar o comportamento de regressão da média. Isto significa que, ao contrário do movimento aleatório padrão ou do movimento de Brown, que pode ser desviado para o infinito, o processo de OU tende a se recuperar ao longo do tempo para a média de longo prazo. Matematicamente, o processo de OU é a solução de uma determinada equação de diferenciação aleatória (SDE) que controla esse comportamento de regressão da média. O SDE do processo de OU é dado pela fórmula:

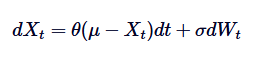
Donde Xt representa um processo aleatório no tempo t, em que μ é o valor médio de longo prazo, θ é o valor médio de regressão, δ é a volatilidade, e dWt é o processo Wiener ou o movimento padrão de Brownian.

Antecedentes históricos e aplicações

O processo Ornstein-Uhlenbeck foi originalmente proposto por Leonard Ornstein e George Eugene Uhlenbeck em 1930 para simular a velocidade de partículas que realizam o movimento de Brownian em condições de atrito. Com o tempo, sua utilidade se estendeu muito além da física, tendo aplicações em diferentes áreas, como biologia, química, economia e finanças.

Em finanças quantitativas, o processo OU é particularmente útil para modelar fenômenos que apresentam um comportamento de regressão da média. Exemplos notáveis incluem os tipos de juros, taxas de câmbio e volatilidade nos mercados financeiros. Por exemplo, o modelo Vasicek, popularmente conhecido como modelo de juros, é derivado diretamente do processo OU.

A importância da quantificação financeira

O processo Ornstein-Uhlenbeck é fundamental para a quantificação financeira, porque sua natureza de regressão do valor médio torna-o uma escolha natural para modelar variáveis financeiras que não apresentam um comportamento aleatório, mas sim flutuações em torno de valores médios de longo prazo estáveis. Esta característica é fundamental para a modelagem de taxas de juros, onde o retorno do valor médio reflete a influência do banco central sobre os níveis de juros estáveis de longo prazo.

Além disso, o processo de OU também é usado em modelos de preços de ativos (incluindo a avaliação de derivativos) e estratégias de gestão de risco. Ele também pode ser usado como bloco de construção para modelos mais complexos, como o modelo Cox-Ingersoll-Ross (CIR), que amplia o processo de OU para modelar taxas de juros não negativas.

Principais características e intuições

As principais características do processo Ornstein-Uhlenbeck podem ser resumidas da seguinte forma:

• A média de regressão:O processo OU tende a regressar à média de longo prazo μ. Isso contrasta com processos como o movimento de Brown, que não apresentam essa tendência.
• A volatilidade:O parâmetro δ controla o nível de aleatoriedade ou volatilidade no processo. Quanto maior a volatilidade, maior o desvio da média antes do processo retornar.
• A velocidade de retorno:O parâmetro θ determina a velocidade de regresso do processo para a média. Quanto maior o valor de θ, mais rápido a velocidade de regresso para a média.
• Estabilidade:O processo de OU é estável, o que significa que suas características estatísticas não mudam com o tempo. Isso é fundamental para a modelagem de sistemas estáveis no setor financeiro.

Intuitivamente, você pode pensar no processo Ornstein-Uhlenbeck como um modelado do comportamento do músculo delgado que se estende em torno do valor médio. Embora o processo possa se desviar do valor médio devido a flutuações aleatórias, a força de tração do músculo delgado (similar ao regresso do valor médio) garante que ele retorne ao valor médio.

Comparação com outros processos aleatórios

Como o processo OU está intimamente relacionado com a modelagem de vários fenômenos financeiros, é frequentemente comparado a outros processos aleatórios (como o movimento de Brown e o movimento de Brown geométrico (GBM)). Ao contrário do movimento de Brown (o movimento de Brown não tem uma tendência de regressão uniforme), o processo OU tem um comportamento de regressão uniforme aparente. Isso o torna mais adequado para modelar cenários em que as variáveis flutuam em torno de um equilíbrio estável.

Em comparação com o GBM, que é normalmente usado para modelar preços de ações e que contém elementos de deriva e volatilidade, o processo OU não apresenta crescimento indiciado, mas sim oscilações em torno de sua média. O GBM é mais adequado para modelar quantidades que crescem com o tempo, enquanto o processo OU é muito adequado para modelar variáveis que apresentam características de regressão da média.

Exemplos de finanças quantitativas

O processo Ornstein-Uhlenbec tem uma ampla aplicação no campo financeiro, especialmente em cenários de modelagem em que a regressão do valor médio é uma característica fundamental.

Modelagem de juros

Uma das aplicações mais proeminentes do processo OU é a modelagem de taxas de juros, especialmente no quadro do modelo Vasicek. O modelo Vasicek assume que as taxas de juros seguem o processo OU, ou seja, que as taxas de juros tendem a retornar à média de longo prazo ao longo do tempo. Esta característica é fundamental para um comportamento de juros analógicos precisos, pois as taxas de juros geralmente não variam indefinidamente, mas em torno de níveis médios, afetados pelas condições econômicas.

Preço dos ativos

No preço de ativos, especialmente em títulos de rendimento fixo, o processo OU é frequentemente usado para simular a evolução dos rendimentos de títulos. A natureza de regressão do valor médio do processo OU garante que os rendimentos não se desviem muito da sua média histórica, o que é consistente com o comportamento observado do mercado. Isso torna o processo OU uma ferramenta valiosa para o preço de títulos e outros instrumentos sensíveis a taxas.

Estratégias de negociação

O processo de OU é particularmente útil, pois pode modelar a diferença de preço entre os dois ativos, que geralmente é um regresso do valor médio. Ao usar o processo de OU para modelar o diferencial de preço, os traders podem identificar pontos de entrada e saída de lucro quando os preços se desviam da sua média, prevendo o regresso do valor médio, gerando assim sinais de negociação.

Por exemplo, se o diferencial entre dois futuros se expandir para além de um determinado limiar, os comerciantes podem fazer um zero de futuros de excelente desempenho e fazer um monte de futuros de baixo desempenho, esperando que o diferencial volte para sua média histórica, tornando-se lucrativo quando a inversão ocorrer.

A resposta de Ornstein-Uhlenbeck SDE

A fórmula da equação diferencial do processo Ornstein-Uhlenbeck é a base para sua solução. Para resolver este SDE, usamos o fator de integração.

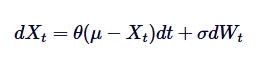
Primeiro, vamos multiplicar ambos os lados pelos fatores de integração. :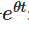

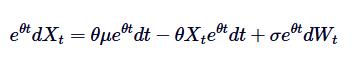
Observe que se somarmos em ambos os lados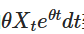A diferença é a diferença de um número de vezes, então a esquerda pode ser representada como a diferença de uma multiplicação:

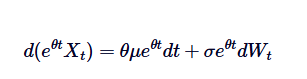
Se você subtrair ambos os lados de 0 para t, você terá:

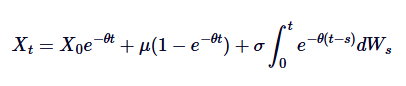
Esta é uma solução geral para Ornstein-Uhlenbeck SDE.

A solução objetiva deduzida acima tem vários significados importantes.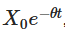Indica o declínio do valor inicial com o tempo e mostra como o processo se torna mais lento e esquece seu início.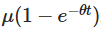O terceiro elemento introduz a aleatoriedade, em que a fração envolvendo o processo de Wiener explica as flutuações aleatórias.

Esta solução enfatiza o equilíbrio entre o comportamento de regressão de equação de certeza e o divisor aleatório impulsionado pelo movimento de Brown. Entender esta solução é fundamental para uma simulação eficaz do processo OU, conforme descrito abaixo.

Ligações com outros processos aleatórios

O processo Ornstein-Uhlenbeck tem várias ligações importantes com outros processos aleatórios conhecidos (incluindo o movimento de Brown e o modelo de Vasicek).

Relacionamento com o movimento Brown

O processo Ornstein-Uhlenbeck pode ser visto como uma versão regressiva do movimento de Brown. O movimento de Brown descreve um processo com uma tendência de incremento independente e sem um movimento de regresso, enquanto o processo de OU introduz um movimento de Brown de média modificado por um elemento de derivação, trazendo o processo de volta ao centro. Matematicamente, se definirmos th = 0, o processo de OU será simplificado para um movimento de Brown padrão com oscilações:

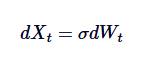
Assim, o movimento browniano é uma exceção do processo OU, correspondendo à ausência de regressão da média.

Relação com o modelo Vasicek

O modelo de Vasicek é amplamente utilizado na modelagem de taxas de juros, sendo essencialmente uma aplicação do processo Ornstein-Uhlenbeck na evolução das taxas de juros. O modelo de Vasicek assume que as taxas de juros seguem o processo OU, em que a SDE é definida como:

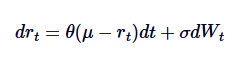
Dentre eles, rt representa a taxa de juros de curto prazo, e a interpretação dos parâmetros θ, μ e δ é semelhante à interpretação no processo de OU. O modelo Vasicek é capaz de produzir um caminho de retorno do valor médio da taxa de juros, que é uma de suas principais vantagens no modelagem financeira.

Compreender essas relações permite uma compreensão mais ampla de como os processos OU são usados em diferentes contextos, especialmente no campo financeiro.

Simulação do processo Ornstein-Uhlenbeck usando Python

Nesta seção, vamos explorar como usar o Python para simular o processo Ornstein-Uhlenbeck (OU). Isso envolve o uso da decomposição de Euler-Maruyama para decompor as equações diferenciais aleatórias (SDE) que definem o processo OU.

Diversificação da SDE

Vamos rever as fórmulas matemáticas do SDE acima e resumir cada um dos termos:

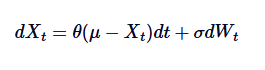
E, em seguida,

• Xt é o valor do processo no tempo t.
• θ é a velocidade de regresso do valor médio.
• μ é a média de longo prazo do processo.
• δ é o parâmetro da taxa de flutuação.
• dWt representa o incremento do processo Wiener (movimento padrão de Brown).

Para simular este processo no computador, é necessário fazer uma dissociação do SDE em tempo contínuo. Um método comumente usado é a dissociação de Euler-Maruyama, que é feita considerando pequenos passos de tempo dissociados.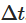A forma discreta do processo Ornstein-Uhlenbeck é dada pela seguinte fórmula:

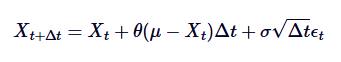
E, em seguida,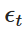É uma variável aleatória extraída da distribuição normal padrão (ou seja,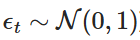Esta descentralização permite-nos calcular o valor de Xt de forma iterativa ao longo do tempo, simulando assim o comportamento do processo OU.

Implementação do Python

Agora vamos implementar o processo Ornstein-Uhlenbeck descentralizado no Python.

Primeiro, nós importamos NumPy e Matplotlib de forma padrão. Então, nós designamos todos os parâmetros para o modelo OU. Então, nós pre-apropriamos um conjunto NumPy de N de comprimento para adicioná-lo a ele depois de calcular o caminho OU. Então nós repetimos o passo N-1 (o passo 1 é a condição inicial de X0 designado), nós simulamos o aumento aleatório DW, e então nós calculamos a próxima geração do caminho OU de acordo com a fórmula matemática acima.

import numpy as np
import matplotlib.pyplot as plt

# Parameters for the OU process
theta = 0.7      # Speed of mean reversion
mu = 0.0         # Long-term mean
sigma = 0.3      # Volatility
X0 = 1.0         # Initial value
T = 10.0         # Total time
dt = 0.01        # Time step
N = int(T / dt)  # Number of time steps

# Pre-allocate array for efficiency
X = np.zeros(N)
X[0] = X0

# Generate the OU process
for t in range(1, N):
    dW = np.sqrt(dt) * np.random.normal(0, 1)
    X[t] = X[t-1] + theta * (mu - X[t-1]) * dt + sigma * dW

# Plot the result
plt.plot(np.linspace(0, T, N), X)
plt.title("Ornstein-Uhlenbeck Process Simulation")
plt.xlabel("Time")
plt.ylabel("X(t)")
plt.show()

Os resultados do desenho são os seguintes:

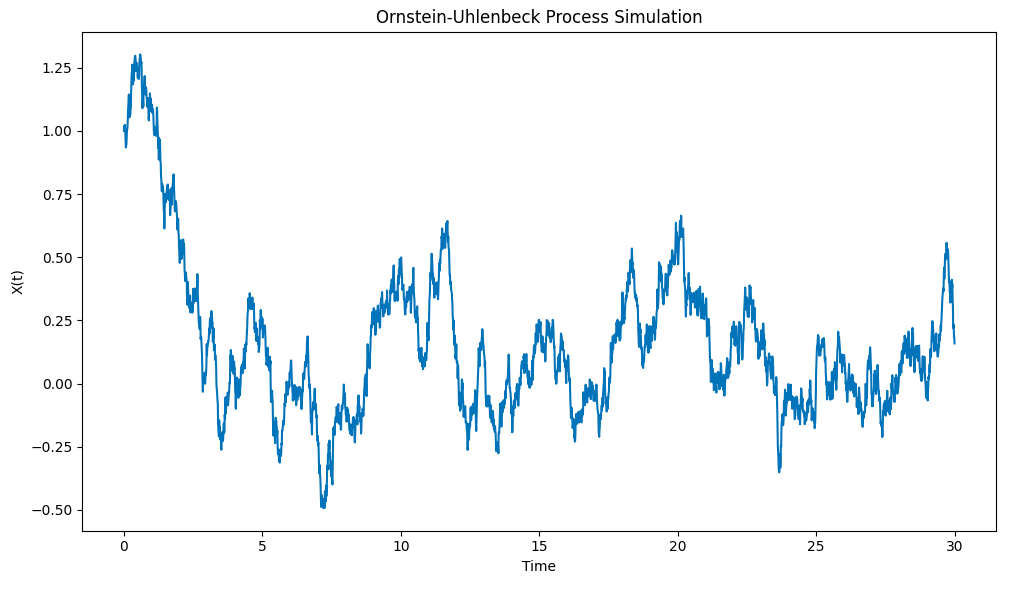
Simulação do processo Ornstein-Uhlenbeck em Python

Observe como o processo puxa rapidamente a coluna X0=1 da condição inicial para o valor médio μ=0, e quando ele se desvia desse valor médio, ele mostra uma tendência de retorno a esse valor médio.

Resumo e seguimento

Neste artigo, descrevemos os processos Ornstein-Uhlenbeck, descrevemos suas fórmulas matemáticas e fornecemos uma implementação básica do Python para simular versões discretas de SDEs de tempo contínuo. Nos artigos seguintes, examinaremos SDEs mais complexas construídas com base em processos OU e como elas podem ser usadas em aplicações de negociação sistêmica e preços de derivativos.

Código completo

# OU process simulation

import numpy as np
import matplotlib.pyplot as plt

# Parameters for the OU process
theta = 0.7      # Speed of mean reversion
mu = 0.0         # Long-term mean
sigma = 0.3      # Volatility
X0 = 1.0         # Initial value
T = 30.0         # Total time
dt = 0.01        # Time step
N = int(T / dt)  # Number of time steps

# Pre-allocate array for efficiency
X = np.zeros(N)
X[0] = X0

# Generate the OU process
for t in range(1, N):
    dW = np.sqrt(dt) * np.random.normal(0, 1)
    X[t] = X[t-1] + theta * (mu - X[t-1]) * dt + sigma * dW

# Plot the result
plt.plot(np.linspace(0, T, N), X)
plt.title("Ornstein-Uhlenbeck Process Simulation")
plt.xlabel("Time")
plt.ylabel("X(t)")
plt.show()

O link original:https://www.quantstart.com/articles/ornstein-uhlenbeck-simulation-with-python/