O modelo de Markov oculto

O modelo de Markov oculto

• 1 - Conhecer

  Hoje vamos apresentar uma simples aplicação do HMM (modelo de Markov) em ações.

  O modelo de Markov oculto, que parece muito sofisticado e que não sabe o que é, vamos dar um passo atrás e ver a cadeia de Markov primeiro.

  A cadeia de Markov, em homenagem a Andrei Markov (A. A. Markov, 1856-1922), é um processo aleatório de eventos dissociados de propriedade de Markov em matemática. Dado o conhecimento ou a informação atual, o passado (ou seja, o estado histórico anterior ao presente) é irrelevante para a previsão do futuro (ou seja, o estado futuro posterior ao presente).

  

  Neste processo, a mudança de cada estado depende apenas dos n estados anteriores, o que é chamado de modelo de um estado n, onde n é o número de estados que afetam a mudança. O processo de Markov mais simples é o processo de um estado, em que a mudança de cada estado depende apenas do estado anterior.

• Dois exemplos.

  A expressão matemática é a seguinte:

  

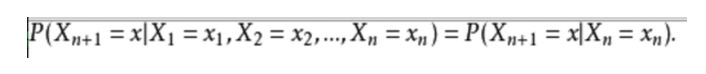
  Para dar um exemplo da vida cotidiana, nós queremos prever o tempo futuro com base nas condições meteorológicas atuais. Uma maneira de fazer isso é assumir que cada estado do modelo depende apenas do estado anterior, ou seja, a hipótese de Markov, que simplifica muito o problema. Claro, este exemplo também é um pouco impraticável.

  

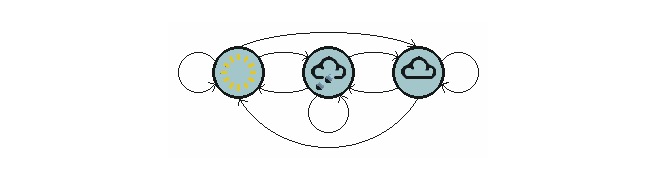
  O gráfico acima mostra um modelo de mudança do tempo.

  Observe que um processo de uma fase contendo N estados tem N2 mudanças de estado. A probabilidade de cada mudança é chamada de probabilidade de mudança de estado, ou seja, a probabilidade de mudança de um estado para outro. Todas essas probabilidades N2 podem ser representadas por uma matriz de mudança de estado, a matriz de mudança de estado do exemplo do tempo acima:

  

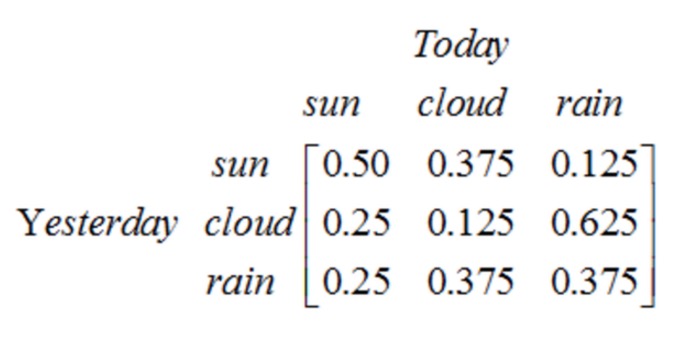
  Esta matriz diz que, se ontem estava nublado, há 25% de probabilidade de que hoje esteja limpo, 12,5% de probabilidade de que esteja nublado, 62,5% de probabilidade de chuva, e obviamente, a soma de cada linha na matriz é um.

  Para iniciar um sistema como esse, precisamos de um vetor de probabilidade inicial:

  

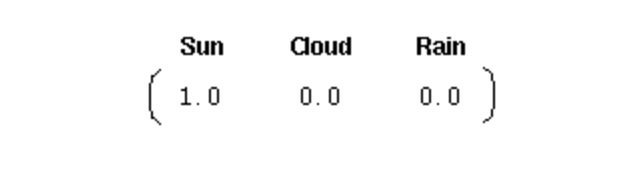
  Este vetor indica que o primeiro dia é de dia limpo. Até aqui, nós definimos as três partes seguintes para o processo Markov de primeira fase acima:

  O estado: tempo limpo, neblina e chuva.

  Vector inicial: define a probabilidade do estado do sistema quando o tempo é zero.

  Matriz de mudança de estado: probabilidade de cada mudança de clima. Todos os sistemas que podem ser descritos dessa forma são processos de Markov.

  No entanto, o que fazer quando o processo de Markov não é suficientemente forte? Em alguns casos, o processo de Markov não é suficiente para descrever os padrões que esperamos encontrar.

  Por exemplo, no nosso mercado de ações, se apenas observarmos o mercado, só podemos saber o preço, o volume de negociação e outras informações do dia, mas não sabemos qual o estado atual do mercado de ações (bull market, bear market, shock, rebound, etc.), nesse caso, temos dois conjuntos de estados, um conjunto de estados observáveis e um conjunto de estados ocultos (stock market status). Esperamos encontrar um algoritmo que possa prever o estado do mercado de ações com base no preço do mercado de ações e no pressuposto de Markov.

  Nesses casos, a sequência de estados observáveis e a sequência de estados ocultos estão relacionados à probabilidade. Assim, podemos modelar esse tipo de processo como um processo de Markov oculto e um conjunto de estados observáveis relacionados à probabilidade desse processo de Markov oculto, o modelo de Markov oculto.

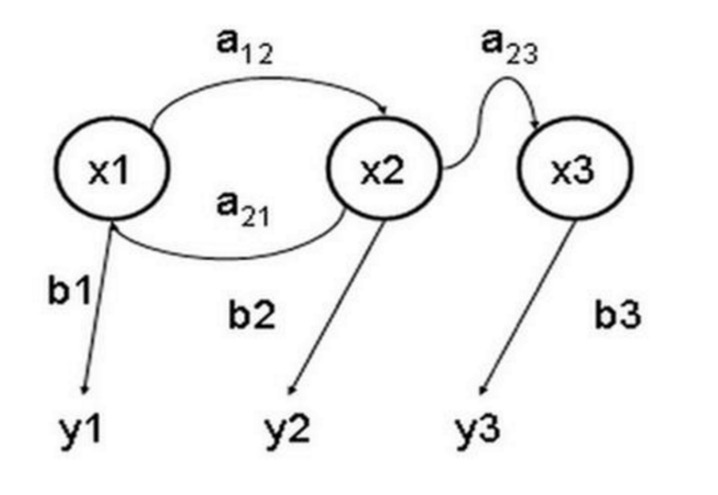
  O modelo oculto de Markov é um modelo estatístico usado para descrever um processo de Markov que contém parâmetros desconhecidos implicitos. A dificuldade é determinar os parâmetros implicitos do processo a partir dos parâmetros observáveis e, em seguida, usar esses parâmetros para uma análise mais aprofundada. A figura abaixo é um diagrama de transferência de estado do modelo oculto de Markov de três estados, onde x representa o estado implicito, y representa a saída observável, a probabilidade de conversão de estado e b a probabilidade de saída.

  

  Explique-se com um exemplo de um casco: Suponha que eu tenha três cascos diferentes na minha mão. O primeiro casco é o nosso casco comum (chamamos este casco de D6), com seis faces, cada uma com uma probabilidade de ocorrência de 1/6. O segundo casco é um quadrado (chamamos este casco de D4), cada uma com uma probabilidade de ocorrência de 1/4.

  

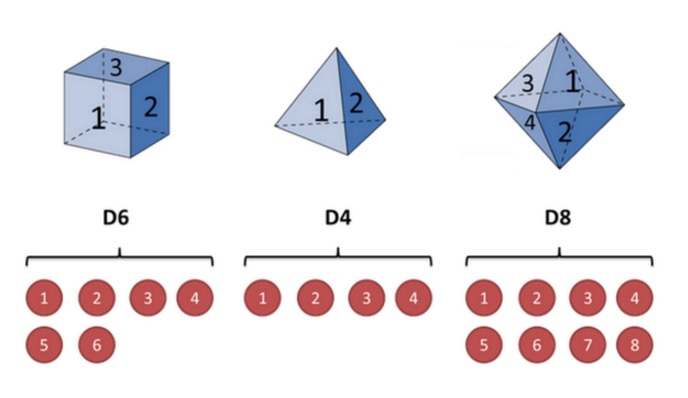
  Suponhamos que começamos o jogo com um dos três jogos e escolhemos um deles, e a probabilidade de cada jogo ser 1/3; então nós escolhemos o jogo, e obtemos um número, um, dois, três, quatro, cinco, seis, sete, oito.

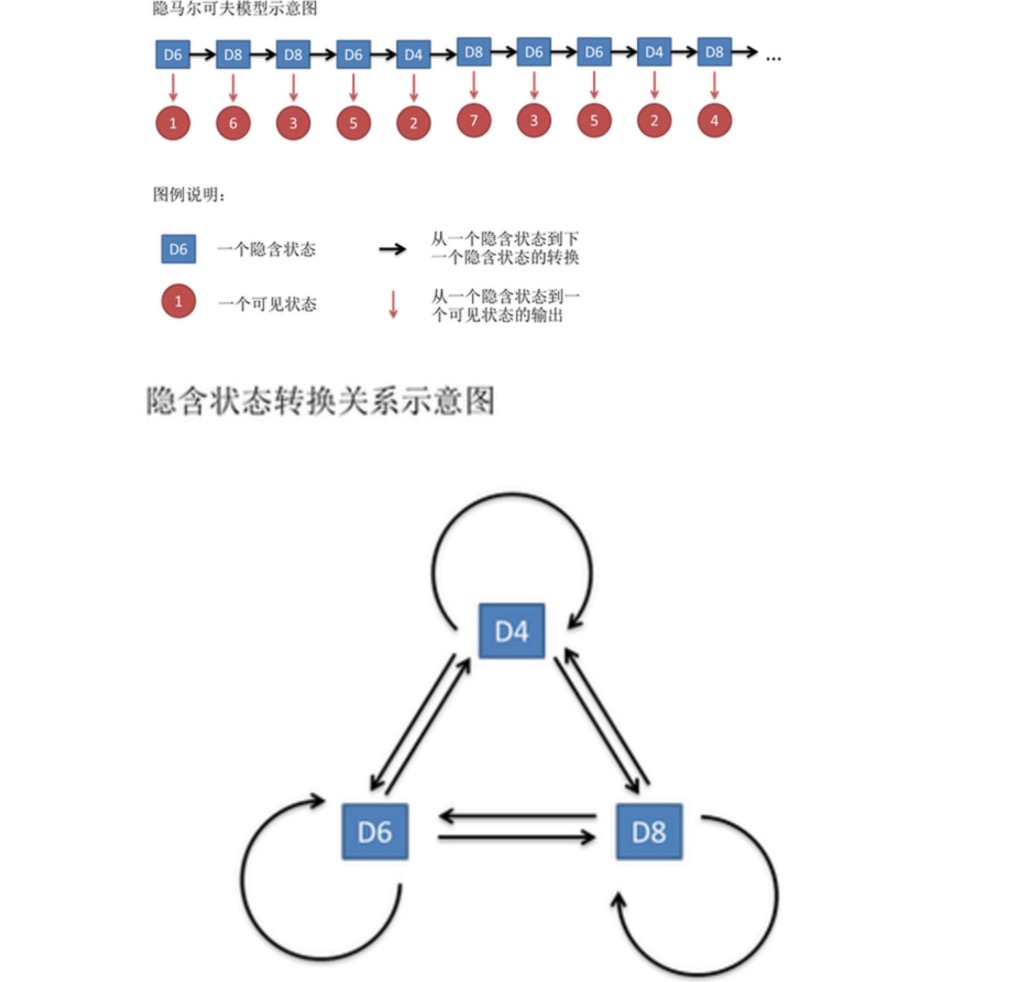
  Esta sequência de números é chamada de cadeia de estado visível. Mas no modelo de Markov oculto, temos não apenas uma cadeia de estado visível, mas também uma cadeia de estado implícita. Neste exemplo, a cadeia de estado implícita é a sequência de cascos que você usa.

  一般来说，HMM中说到的马尔可夫链其实是指隐含状态链，因为隐含状态（骰子）之间存在转换概率。在我们这个例子里，D6的下一个状态是D4，D6，D8的概率都是1/3。D4，D8的下一个状态是D4，D6，D8的转换概率也都一样是1/3。这样设定是为了最开始容易说清楚，但是我们其实是可以随意设定转换概率的。比如，我们可以这样定义，D6后面不能接D4，D6后面是D6的概率是0.9，是D8的概率是0.1。这样就是一个新的HMM。

  Da mesma forma, embora não haja uma probabilidade de conversão entre os estados visíveis, há uma probabilidade entre os estados implícitos e os visíveis chamada probabilidade de saída. No nosso exemplo, a probabilidade de saída de um hexadecimal (D6) é 1/6. A probabilidade de saída de um hexadecimal (D6) é 1/6. A probabilidade de saída de um hexadecimal (D6) é 1/6.

  

  Na verdade, para o HMM, é bastante fácil fazer uma simulação se você souber com antecedência a probabilidade de conversão entre todos os estados implícitos e a probabilidade de saída entre todos os estados implícitos e todos os estados visíveis. Mas, quando se aplica o modelo HMM, muitas vezes falta uma parte da informação, às vezes você sabe que há vários tipos de cascos, o que é cada casco, mas não sabe a sequência de cascos extraídos; às vezes você só vê o resultado de muitos cascos e não sabe nada sobre o restante.

  Os algoritmos relacionados ao modelo HMM são divididos em três categorias principais, resolvendo três problemas:

  • Sabendo que existem vários tipos de macacos (quantidade de estados implícitos), o que é cada tipo de macaco (probabilidade de conversão), e de acordo com o resultado do lançamento do macaco (cadeia de estados visível), quero saber qual é o tipo de macaco que é lançado cada vez (cadeia de estados implícitos).

  • Também sei que existem vários tipos de macacos (quantidade de estados implícitos), o que é cada tipo de macaco (probabilidade de conversão) e, com base no resultado do macaco (cadeia de estados visível), quero saber a probabilidade de obter esse resultado.

  • Sabendo que existem vários tipos de macacos (quantidade de estados implícitos), sem saber o que é cada tipo de macaco (probabilidade de conversão), observando o resultado de muitos tipos de macacos (cadeia de estados visível), eu quero inverter o que é cada tipo de macaco (probabilidade de conversão).

    Se quisermos resolver o problema da bolsa, precisamos resolver o problema 1 e o problema 3, e no próximo artigo veremos como isso acontece.

Traduzido da coluna sobre Moneycode