Estratégia de Média Móvel Adaptativa do Canal Gaussiano
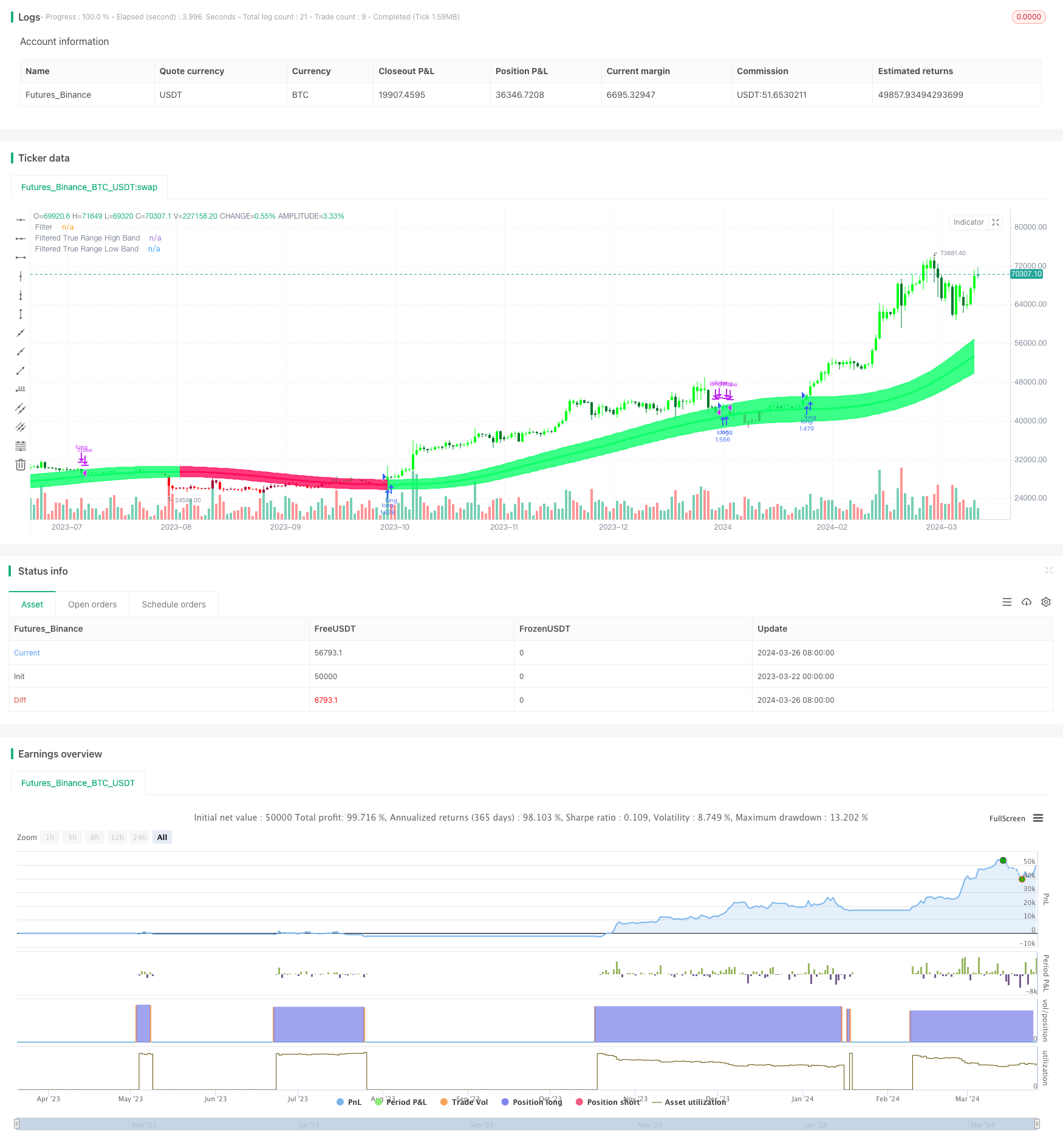
Visão geral
A estratégia de equilíbrio auto-adaptável do canal de Gauss é uma estratégia de negociação quantitativa que utiliza a técnica de Gauss e a configuração de parâmetros auto-adaptáveis. A estratégia é baseada na teoria de Gauss, proposta por John Ehlers, e gera um sinal de negociação suave e adaptável através da multiplicação da média móvel do índice de dados de preços. O núcleo da estratégia é a construção de um canal de preços ajustado dinamicamente, obtendo a amplitude de oscilação real após o aumento e diminuição do preço após a onda de Gauss.
Princípio da estratégia
O princípio da estratégia de auto-adaptação do canal de Gauss é o seguinte:
- Calcule o valor de Gauss para o preço. Calcule os parâmetros Beta e Alpha de acordo com o período de amostragem e o número de pontos polares definidos pelo usuário, depois faça a escala de Gauss para os dados de preço e obtenha uma sequência de preços de processamento suave.
- Calcule o valor de Gauss para a amplitude real. Faça o mesmo tratamento de Gauss para a amplitude real dos preços, obtendo uma sequência de amplitudes de fluxo suave.
- Construção de um canal de Gauss. Com o preço de Gauss após a onda de choque, o canal superior é formado pelo canal médio mais a amplitude de onda real multiplicada pelo número de vezes o valor definido pelo usuário, e o canal inferior é formado pelo canal médio menos esse valor, formando um canal dinâmico.
- Geração de sinais de negociação. Quando o preço sobe, ele gera um sinal de compra; quando o preço desce, ele gera um sinal de venda.
- Introdução de um parâmetro de período de tempo. O usuário pode configurar a hora de início e término da execução da estratégia, dentro do período de tempo em que a estratégia opera de acordo com o sinal de negociação.
Análise de vantagens
A estratégia de equilíbrio de adaptação do canal de Gauss tem as seguintes vantagens:
- A estratégia utiliza parâmetros de ajuste dinâmico, que podem ser adaptados a diferentes estados de mercado e variedades de negociação, sem a necessidade de debug manual frequente.
- A estratégia é capaz de capturar e acompanhar melhor as tendências do mercado, evitando sinais falsos em mercados de turbulência, através da construção de canais de preços.
- Boa suavização. O uso da técnica de ondas de Gauss para processar os dados de preços de forma suave, removendo a maior parte do ruído do mercado, fazendo com que os sinais de negociação sejam mais confiáveis.
- Alta flexibilidade. O usuário pode ajustar os parâmetros da estratégia de acordo com a necessidade, como o período de amostragem, o número de pólos, o múltiplo de oscilação, etc., para otimizar o desempenho da estratégia.
- Introdução de parâmetros de período de tempo, permitindo que a estratégia possa ser executada em intervalos de tempo especificados, facilitando a aplicação em campo e o estudo de retrospecção.
Análise de Riscos
Embora a estratégia de auto-adaptação do Canal de Gauss tenha muitos benefícios, há alguns riscos:
- Riscos de configuração de parâmetros. A configuração inadequada de parâmetros pode levar à falha ou mau desempenho da estratégia, portanto, é necessário testar e otimizar repetidamente na aplicação real.
- Risco de acidentes. A estratégia pode não reagir adequadamente em tempo hábil para alguns acidentes importantes, causando prejuízos.
- Risco de sobreajuste. Se os parâmetros forem ajustados demais para os dados históricos, a estratégia pode ter um desempenho ruim no futuro, e o desempenho interno e externo da amostra deve ser levado em consideração.
- Risco de arbitragem. A estratégia é aplicada principalmente em mercados tendenciais, onde o risco de arbitragem pode ser maior se você negociar com frequência em mercados turbulentos.
Direção de otimização
A estratégia de auto-adaptação do Canal de Gauss inclui:
- Otimização de parâmetros dinâmicos. Otimização automática e ajuste dinâmico de parâmetros de estratégia, melhorando a adaptabilidade, através da introdução de tecnologias como aprendizado de máquina.
- Fusão de múltiplos fatores: combinação de outros indicadores ou fatores técnicos eficazes com o canal de Gauss para formar um sinal de negociação mais robusto.
- Optimizar o gerenciamento de posições. Adicionar regras razoáveis de gerenciamento de posições e gerenciamento de fundos com base na estratégia, controlar o retorno e o risco.
- Multi-variedade de colaboração: a estratégia é estendida para várias variedades de negociação diferentes, para dispersar o risco por meio da configuração de ativos e análise de correlação.
Resumir
A estratégia de equilíbrio de auto-adaptação do canal de Gauss é uma estratégia de negociação quantitativa baseada em ondas de Gauss e parâmetros de auto-adaptação para gerar sinais de negociação confiáveis e suaves por meio da construção dinâmica de canais de preços. A estratégia possui vantagens como boa adaptabilidade, boa traçabilidade de tendências, alta flexibilidade, grande flexibilidade e forte praticidade, mas também enfrenta o risco de configuração de parâmetros, eventos surpreendentes, superalimento e arbitragem.
/*backtest
start: 2023-03-22 00:00:00
end: 2024-03-27 00:00:00
period: 1d
basePeriod: 1h
exchanges: [{"eid":"Futures_Binance","currency":"BTC_USDT"}]
*/
//@version=4
strategy(title="Gaussian Channel Strategy v1.0", overlay=true, calc_on_every_tick=false, initial_capital=10000, default_qty_type=strategy.percent_of_equity, default_qty_value=100, commission_type=strategy.commission.percent, commission_value=0.1)
// Date condition inputs
startDate = input(title="Date Start", type=input.time, defval=timestamp("1 Jan 2018 00:00 +0000"), group="Dates")
endDate = input(title="Date End", type=input.time, defval=timestamp("31 Dec 2060 23:59 +0000"), group="Dates")
timeCondition = true
// This study is an experiment utilizing the Ehlers Gaussian Filter technique combined with lag reduction techniques and true range to analyze trend activity.
// Gaussian filters, as Ehlers explains it, are simply exponential moving averages applied multiple times.
// First, beta and alpha are calculated based on the sampling period and number of poles specified. The maximum number of poles available in this script is 9.
// Next, the data being analyzed is given a truncation option for reduced lag, which can be enabled with "Reduced Lag Mode".
// Then the alpha and source values are used to calculate the filter and filtered true range of the dataset.
// Filtered true range with a specified multiplier is then added to and subtracted from the filter, generating a channel.
// Lastly, a one pole filter with a N pole alpha is averaged with the filter to generate a faster filter, which can be enabled with "Fast Response Mode".
//Custom bar colors are included.
//Note: Both the sampling period and number of poles directly affect how much lag the indicator has, and how smooth the output is.
// Larger inputs will result in smoother outputs with increased lag, and smaller inputs will have noisier outputs with reduced lag.
// For the best results, I recommend not setting the sampling period any lower than the number of poles + 1. Going lower truncates the equation.
//-----------------------------------------------------------------------------------------------------------------------------------------------------------------
//Updates:
// Huge shoutout to @e2e4mfck for taking the time to improve the calculation method!
// -> migrated to v4
// -> pi is now calculated using trig identities rather than being explicitly defined.
// -> The filter calculations are now organized into functions rather than being individually defined.
// -> Revamped color scheme.
//-----------------------------------------------------------------------------------------------------------------------------------------------------------------
//Functions - courtesy of @e2e4mfck
//-----------------------------------------------------------------------------------------------------------------------------------------------------------------
//Filter function
f_filt9x (_a, _s, _i) =>
int _m2 = 0, int _m3 = 0, int _m4 = 0, int _m5 = 0, int _m6 = 0,
int _m7 = 0, int _m8 = 0, int _m9 = 0, float _f = .0, _x = (1 - _a)
// Weights.
// Initial weight _m1 is a pole number and equal to _i
_m2 := _i == 9 ? 36 : _i == 8 ? 28 : _i == 7 ? 21 : _i == 6 ? 15 : _i == 5 ? 10 : _i == 4 ? 6 : _i == 3 ? 3 : _i == 2 ? 1 : 0
_m3 := _i == 9 ? 84 : _i == 8 ? 56 : _i == 7 ? 35 : _i == 6 ? 20 : _i == 5 ? 10 : _i == 4 ? 4 : _i == 3 ? 1 : 0
_m4 := _i == 9 ? 126 : _i == 8 ? 70 : _i == 7 ? 35 : _i == 6 ? 15 : _i == 5 ? 5 : _i == 4 ? 1 : 0
_m5 := _i == 9 ? 126 : _i == 8 ? 56 : _i == 7 ? 21 : _i == 6 ? 6 : _i == 5 ? 1 : 0
_m6 := _i == 9 ? 84 : _i == 8 ? 28 : _i == 7 ? 7 : _i == 6 ? 1 : 0
_m7 := _i == 9 ? 36 : _i == 8 ? 8 : _i == 7 ? 1 : 0
_m8 := _i == 9 ? 9 : _i == 8 ? 1 : 0
_m9 := _i == 9 ? 1 : 0
// filter
_f := pow(_a, _i) * nz(_s) +
_i * _x * nz(_f[1]) - (_i >= 2 ?
_m2 * pow(_x, 2) * nz(_f[2]) : 0) + (_i >= 3 ?
_m3 * pow(_x, 3) * nz(_f[3]) : 0) - (_i >= 4 ?
_m4 * pow(_x, 4) * nz(_f[4]) : 0) + (_i >= 5 ?
_m5 * pow(_x, 5) * nz(_f[5]) : 0) - (_i >= 6 ?
_m6 * pow(_x, 6) * nz(_f[6]) : 0) + (_i >= 7 ?
_m7 * pow(_x, 7) * nz(_f[7]) : 0) - (_i >= 8 ?
_m8 * pow(_x, 8) * nz(_f[8]) : 0) + (_i == 9 ?
_m9 * pow(_x, 9) * nz(_f[9]) : 0)
//9 var declaration fun
f_pole (_a, _s, _i) =>
_f1 = f_filt9x(_a, _s, 1), _f2 = (_i >= 2 ? f_filt9x(_a, _s, 2) : 0), _f3 = (_i >= 3 ? f_filt9x(_a, _s, 3) : 0)
_f4 = (_i >= 4 ? f_filt9x(_a, _s, 4) : 0), _f5 = (_i >= 5 ? f_filt9x(_a, _s, 5) : 0), _f6 = (_i >= 6 ? f_filt9x(_a, _s, 6) : 0)
_f7 = (_i >= 2 ? f_filt9x(_a, _s, 7) : 0), _f8 = (_i >= 8 ? f_filt9x(_a, _s, 8) : 0), _f9 = (_i == 9 ? f_filt9x(_a, _s, 9) : 0)
_fn = _i == 1 ? _f1 : _i == 2 ? _f2 : _i == 3 ? _f3 :
_i == 4 ? _f4 : _i == 5 ? _f5 : _i == 6 ? _f6 :
_i == 7 ? _f7 : _i == 8 ? _f8 : _i == 9 ? _f9 : na
[_fn, _f1]
//-----------------------------------------------------------------------------------------------------------------------------------------------------------------
//Inputs
//-----------------------------------------------------------------------------------------------------------------------------------------------------------------
//Source
src = input(defval=hlc3, title="Source")
//Poles
int N = input(defval=4, title="Poles", minval=1, maxval=9)
//Period
int per = input(defval=144, title="Sampling Period", minval=2)
//True Range Multiplier
float mult = input(defval=1.414, title="Filtered True Range Multiplier", minval=0)
//Lag Reduction
bool modeLag = input(defval=false, title="Reduced Lag Mode")
bool modeFast = input(defval=false, title="Fast Response Mode")
//-----------------------------------------------------------------------------------------------------------------------------------------------------------------
//Definitions
//-----------------------------------------------------------------------------------------------------------------------------------------------------------------
//Beta and Alpha Components
beta = (1 - cos(4*asin(1)/per)) / (pow(1.414, 2/N) - 1)
alpha = - beta + sqrt(pow(beta, 2) + 2*beta)
//Lag
lag = (per - 1)/(2*N)
//Data
srcdata = modeLag ? src + (src - src[lag]) : src
trdata = modeLag ? tr(true) + (tr(true) - tr(true)[lag]) : tr(true)
//Filtered Values
[filtn, filt1] = f_pole(alpha, srcdata, N)
[filtntr, filt1tr] = f_pole(alpha, trdata, N)
//Lag Reduction
filt = modeFast ? (filtn + filt1)/2 : filtn
filttr = modeFast ? (filtntr + filt1tr)/2 : filtntr
//Bands
hband = filt + filttr*mult
lband = filt - filttr*mult
// Colors
color1 = #0aff68
color2 = #00752d
color3 = #ff0a5a
color4 = #990032
fcolor = filt > filt[1] ? #0aff68 : filt < filt[1] ? #ff0a5a : #cccccc
barcolor = (src > src[1]) and (src > filt) and (src < hband) ? #0aff68 : (src > src[1]) and (src >= hband) ? #0aff1b : (src <= src[1]) and (src > filt) ? #00752d :
(src < src[1]) and (src < filt) and (src > lband) ? #ff0a5a : (src < src[1]) and (src <= lband) ? #ff0a11 : (src >= src[1]) and (src < filt) ? #990032 : #cccccc
//-----------------------------------------------------------------------------------------------------------------------------------------------------------------
//Outputs
//-----------------------------------------------------------------------------------------------------------------------------------------------------------------
//Filter Plot
filtplot = plot(filt, title="Filter", color=fcolor, linewidth=3)
//Band Plots
hbandplot = plot(hband, title="Filtered True Range High Band", color=fcolor)
lbandplot = plot(lband, title="Filtered True Range Low Band", color=fcolor)
//Channel Fill
fill(hbandplot, lbandplot, title="Channel Fill", color=fcolor, transp=80)
//Bar Color
barcolor(barcolor)
longCondition = crossover(close, hband) and timeCondition
closeAllCondition = crossunder(close, hband) and timeCondition
if longCondition
strategy.entry("long", strategy.long)
if closeAllCondition
strategy.close("long")