Симуляция Орнштейна-Уленбека с помощью Python

В этой статье мы рассмотрим процесс Орнштейна-Ухленбека, опишем его математические формулы, реализуем и смоделируем его с помощью Python, и обсудим некоторые практические применения в количественной финансовой и системной торговле. Мы будем использовать более продвинутую модель случайного процесса, называемую процессом Орнштейна-Ухленбека (OU), которая может быть использована для моделирования временных последовательностей, характеризующих равнозначные регрессии. Это особенно полезно для моделирования процентных ставок в цене деривативов и для алгоритмов системной торговли при торговле.

Что такое процесс Орнштейна-Уленбека?

Процесс Орнштейна-Уленбека - это последовательный временной случайный процесс, используемый для моделирования поведения уравнительных регрессий. Это означает, что, в отличие от стандартного случайного блуждания или движения Брауна, которые могут дрейфовать бесконечно, процесс ОУ часто восстанавливается со временем до долгосрочных средних. Математически, процесс ОУ является решением конкретного случайного дифференциального уравнения (SDE), которое контролирует такое уравнительное регрессивное поведение.

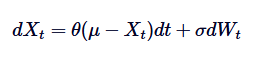
Здесь Xt обозначает случайный процесс в t времени, где μ - длительный средний, θ - средний уровень регрессии, δ - волатильность, а dWt - процесс Вейнера или стандартное движение Брауна.

Исторический контекст и применение

Процесс Орнштейна-Ухленбека был первоначально предложен Леонардом Орнштейном и Джорджем Юдженом Ухленбеком в 1930 году для моделирования скорости частиц, движущихся при трении. Со временем его полезность вышла далеко за рамки физики и имеет применение в различных областях, таких как биология, химия, экономика и финансы.

В количественных финансах процесс ОУ особенно полезен для моделирования явлений, которые демонстрируют регрессивное поведение средних значений. Примечательными примерами являются волатильность процентных ставок, обменных курсов и финансовых рынков.

Важность количественного финансирования

Процесс Орнштейна-Уленбека имеет важное значение в количественной финансовой системе, по следующим причинам. Его естественный характер, связанный с возвратом средней величины, делает его естественным выбором для моделирования финансовых переменных, которые не проявляют случайного движения, а колеблются вокруг стабильных долгосрочных средних.

Кроме того, OU-процесс используется в моделях ценообразования активов (включая оценку деривативов) и стратегии управления рисками. Он также может служить строительным блоком более сложных моделей, таких как модель Кокса-Ингерсолла-Росса (CIR), которая расширяет процесс OU для моделирования неотрицательных процентных ставок.

Основные характеристики и интуиция

Основные характеристики процесса Орнштейна-Уленбека могут быть обобщены следующим образом:

• Уровень регрессии:Процессы OU склонны к возвращению к длительному среднему значению μ. Это в отличие от процессов, таких как движение Брауна, которые не демонстрируют такой тенденции.
• Волатильность:Уровень случайности или волатильности в процессе, контролируемом параметром δ. Чем выше волатильность, тем больше отклонение от среднего значения до регрессии процесса.
• Скорость возвращения:Параметр θ определяет скорость, с которой процесс возвращается к среднему значению. Чем выше значение θ, тем быстрее возвращается среднее значение.
• Стабильность:Процесс ОУ является плавным, что означает, что его статистические характеристики не меняются с течением времени. Это важно для моделирования стабильных систем в финансовом секторе.

Интуитивно вы можете рассматривать процесс Орнштейна-Ухленбека как моделирование поведения кожицы, которая растягивается вокруг среднего значения. Хотя процесс может отклоняться от равновесия из-за случайных колебаний, тяговая сила кожицы (похожая на равновесное возвращение) гарантирует, что она в конечном итоге вернется к равновесию.

Сравнение с другими случайными процессами

Поскольку OU-процессы тесно связаны с моделированием различных финансовых явлений, их часто сравнивают с другими случайными процессами (например, движением Брауна и геометрическим движением Брауна (GBM)).

В отличие от GBM, который обычно используется для моделирования цен на акции и включает в себя дрейф и волатильность, OU-процесс не демонстрирует индексного роста, а колеблется вокруг его среднего значения. GBP лучше подходит для моделирования количества, которое растет с течением времени, а OU-процесс идеально подходит для моделирования переменных, которые показывают характеристики среднего regression.

Примеры количественного финансирования

Процесс Орнштейна-Уленбека имеет широкое применение в финансовой сфере, особенно в модельных сценариях, где возвращение средних значений является ключевой характеристикой. Ниже мы рассмотрим некоторые из наиболее распространенных случаев использования.

Моделирование процентных ставок

Одно из наиболее ярких применений процесса OU - моделирование процентных ставок, особенно в рамках модели Васицека. Модель Васицека предполагает, что процентные ставки следуют процессу OU, т.е. что процентные ставки часто возвращаются к долгосрочным средним с течением времени. Эта особенность важна для точного моделирования поведения процентных ставок, поскольку процентные ставки часто не колеблются бесконечно, а колеблются вблизи среднего уровня, под влиянием экономических условий.

Ценообразование активов

В ценообразовании активов, особенно фиксированных ценных бумаг, OU-процессы обычно используются для моделирования эволюции доходности облигаций. Уравнительно-регрессивная природа OU-процессов гарантирует, что доходы не будут слишком сильно отклоняться от их исторических средних, что соответствует наблюдаемому рыночному поведению.

Сочетание стратегий торговли

Совместная торговля - это нейтральная стратегия, которая предполагает создание позиций в двух соответствующих активах. В этом случае OU-процесс особенно полезен, поскольку он может моделировать разницу в ценах между двумя активами, при этом разница обычно является возвратом среднего значения.

Например, если разница между двумя фьючерсами расширяется до превышения определенного порога, то трейдеры могут обменять отличные фьючерсы на плохие фьючерсы, ожидая, что разница вернется к их историческим средним, что приведет к прибыли в случае переворота.

Ответы Ornstein-Uhlenbeck SDE

Формулы дифференциальных уравнений процесса Орнштейна-Уленбека являются основой для его решения. Для решения этого SDE мы использовали теорию интегральных факторов. Давайте перепишем SDE:

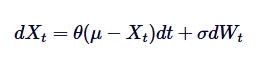
Во-первых, мы умножим обе стороны на множители. :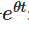

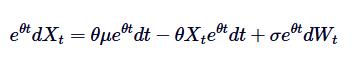
Обратите внимание, что если мы сложим обе стороны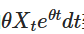Если вы видите, что у вас есть один из этих вариантов, то вы видите, что у вас есть два варианта.

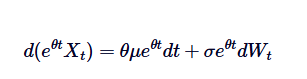
Если мы положим обе стороны от 0 до t, мы получим:

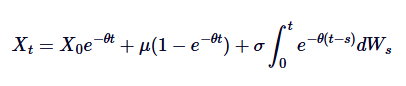
Это общее решение Ornstein-Uhlenbeck SDE.

Выводы, сделанные выше, имеют несколько важных значений.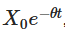Означает, что начальное значение со временем уменьшается, и показывает, как процесс постепенно забывает о своем начале.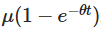Указывает, что процесс с течением времени имеет тенденцию к среднему значению μ. Третий пункт вводит случайность, в которой компоненты, связанные с процессом Wiener, объясняют случайные колебания.

Это решение подчеркивает баланс между равнозначным regression поведением определенности и драйвером движения Брауна. Понимание этого решения имеет решающее значение для эффективного моделирования процессов OU, как описано ниже.

Связь с другими случайными процессами

Процесс Орнштейна-Уленбека имеет ряд важных связей с другими известными случайными процессами (включая движение Брауна и модель Васикека).

Отношения с движением Браун

Процесс Орнштейна-Ухленбека можно рассматривать как уравнительную регрессию движения Брауна. Движение Брауна описывает процесс, который имеет тенденцию с независимым увеличением и без уравнения регрессии, а процесс ОУ вводит уравнительную регрессию движения Брауна с помощью модификации дефляции, что заставляет процесс тянуться обратно к центру. Математически, если мы установимθ=0, процесс ОУ упрощается до стандартного движения Брауна с колебаниями:

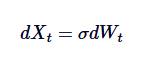
Таким образом, движение Брауна является исключением процесса OU, который соответствует отсутствию regression средних значений.

Отношения с моделью Васичек

Васичекская модель широко используется в моделировании процентных ставок, по сути, это применение процесса Орнштейна-Уленбека в эволюции процентных ставок. Васичекская модель предполагает, что процентные ставки следуют процессу OU, где SDE определяется как:

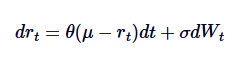
Из них rt обозначает краткосрочные процентные ставки, а интерпретация параметров θ, μ и δ аналогична интерпретации в процессе OU. Модель Васицека способна генерировать равнозначные регрессивные пути процентных ставок, что является одним из ее основных преимуществ в финансовой моделировании.

Понимание этих связей позволяет получить более широкое понимание того, как процессы ОУ используются в различных средах, особенно в финансовой сфере. Мы рассмотрим их практическое значение, когда обсудим примеры применения ниже.

Симуляция процесса Ornstein-Uhlenbeck с помощью Python

В этом разделе мы рассмотрим, как использовать Python для моделирования процессов Ornstein-Uhlenbeck (OU). Это включает использование дифференциации Euler-Maruyama для дифференциации случайных дифференциальных уравнений (SDE), определяющих процессы OU.

Дискриминация SDE

Давайте рассмотрим математические формулы SDE выше и обобщим каждый из них:

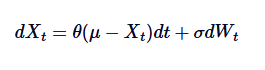
В том числе:

• Xt - это значение процесса во время t.
• θ - скорость возвращения уравнения.
• М - длительный средний для процесса.
• δ - параметр колебания.
• dWt обозначает прирост процесса Wiener (стандартный движение Брауна).

Чтобы смоделировать этот процесс на компьютере, нам необходимо дифференцировать SDE в непрерывном времени. Один из распространенных методов - дифференцирование Эйлера-Маруямы, которое удлиняется, учитывая небольшие шаги в дифференцированном времени.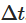Приблизительно непрерывный процесс. Диссонантная форма процесса Орнштейна-Уленбека дается следующим образом:

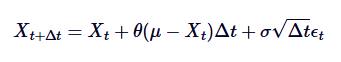
В том числе: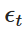Это случайная переменная, извлеченная из стандартного нормального распределения, т.е.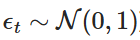) ; такая дифференциация позволяет нам периодически вычислять значение Xt с течением времени, имитируя поведение процесса OU.

Реализация Python

Теперь давайте реализуем децентрализованный процесс Орнштейна-Уленбека с помощью Python. Ниже мы будем использовать только библиотеки NumPy и Matplotlib Python.

Сначала мы вводим NumPy и Matplotlib в стандартном порядке. Затем мы указываем все параметры модели OU. Затем мы заранее выделяем N-длину NumPy, чтобы добавить ее к ней после вычисления пути OU. Затем мы повторяем N-1 шаг (шаг 1 является начальным условием назначения X0), моделируем произвольное увеличение DW, а затем вычисляем следующий разряд пути OU в соответствии с вышеуказанными математическими формулами.

import numpy as np
import matplotlib.pyplot as plt

# Parameters for the OU process
theta = 0.7      # Speed of mean reversion
mu = 0.0         # Long-term mean
sigma = 0.3      # Volatility
X0 = 1.0         # Initial value
T = 10.0         # Total time
dt = 0.01        # Time step
N = int(T / dt)  # Number of time steps

# Pre-allocate array for efficiency
X = np.zeros(N)
X[0] = X0

# Generate the OU process
for t in range(1, N):
    dW = np.sqrt(dt) * np.random.normal(0, 1)
    X[t] = X[t-1] + theta * (mu - X[t-1]) * dt + sigma * dW

# Plot the result
plt.plot(np.linspace(0, T, N), X)
plt.title("Ornstein-Uhlenbeck Process Simulation")
plt.xlabel("Time")
plt.ylabel("X(t)")
plt.show()

Результаты рисунка показывают:

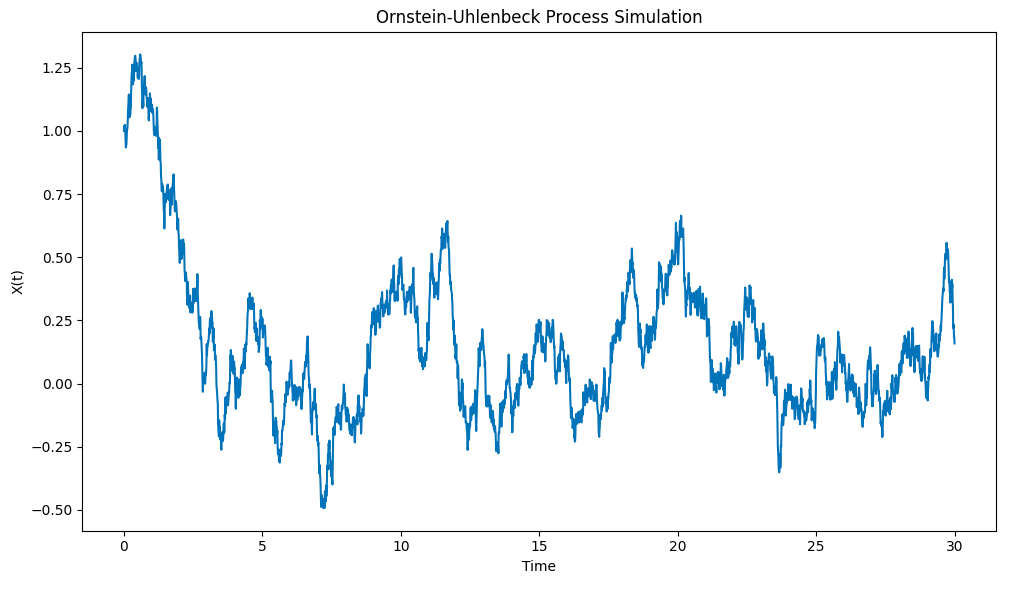
Симуляция процесса Ornstein-Uhlenbeck, выполненная с помощью Python

Обратите внимание на то, как процесс быстро вытаскивает хем X0=1 из исходных условий к среднему значению μ=0, а затем, когда он отклоняется от этого среднего, он показывает тенденцию к возвращению к этому среднему значению.

Резюме и дальнейшие шаги

В этой статье мы объясняем процессы Ornstein-Uhlenbeck, описываем их математические формулы и предоставляем базовые реализации Python для моделирования дискретной версии SDE непрерывного времени. В последующих статьях мы рассмотрим более сложные SDE, построенные на основе процессов OU, и узнаем, как они могут использоваться в системных торговых и производных ценовых приложениях.

Полный код

# OU process simulation

import numpy as np
import matplotlib.pyplot as plt

# Parameters for the OU process
theta = 0.7      # Speed of mean reversion
mu = 0.0         # Long-term mean
sigma = 0.3      # Volatility
X0 = 1.0         # Initial value
T = 30.0         # Total time
dt = 0.01        # Time step
N = int(T / dt)  # Number of time steps

# Pre-allocate array for efficiency
X = np.zeros(N)
X[0] = X0

# Generate the OU process
for t in range(1, N):
    dW = np.sqrt(dt) * np.random.normal(0, 1)
    X[t] = X[t-1] + theta * (mu - X[t-1]) * dt + sigma * dW

# Plot the result
plt.plot(np.linspace(0, T, N), X)
plt.title("Ornstein-Uhlenbeck Process Simulation")
plt.xlabel("Time")
plt.ylabel("X(t)")
plt.show()

Ссылка на текст:https://www.quantstart.com/articles/ornstein-uhlenbeck-simulation-with-python/