赌徒的交易策略

赌徒的交易策略

本文的实践内容可参照马克.沃尔伯格的最新电影《赌徒/The Gambler 2014》。本文的主题其实就是乔布斯曾说过一句话：“我们减少随机性，藉此让人们感受到多一点的随机 (We’re making it less random to make it feel more random)。

伦敦交易员注：以下几段为前言，小编建议先耐心看完前言再阅读正文，这样能更好得体会乔帮主的高明。

• 美国独立宣言里最常被荧光笔划起来的句子莫过于：“人生而平等 (All men are created equal)。”然而与其说是陈述“事实”，这句话更接近我们去庙里拜拜时低头呢喃的“许愿”：我们希望人人生而平等。

  许愿暗示这件事是不存在的：有人从婴儿车就开奔驰，有人IQ180，三岁就用毛笔算微积分还写瘦金体。遇到这些人，我们唯一能做的只有想方设法替来世积德。

  今天要讨论的不平等，比上面这些更令人感到不平衡：为什么总有人能一直中奖！

  每间公司总有几位这样的人，每次年会抽奖都腼腆地上台领奖，说是被财神附身也不为过。我曾经买咖啡中了买1送1，拿到送的打开，又是买1送1，晚上兴奋得睡不着觉(当然，也可能是摄取过多咖啡因)。

  这是唯一能称之为连续中奖的经验。

  连续中奖是件不公平的事，永远发生在“别人”身上

  假设公司有200人，年会抽奖中头奖的机率是1/200=0.5%，连续2年中头奖的机率是0.5%×0.5%=百万分之二十五，够低吧。

  但事实上这是特定某人(你)连续2年中头奖的机率。任何1个人连续2年中头奖的机率是200×0.5%×0.5%=0.5%，跟你抽中1次头奖的机率相等。

  放宽一点，3年内有一个人中奖2次的机率呢：1 - 3年3位不同中奖者的机率=1-200×199×198/(200×200×200)=1.5%

  跟你3年内中1次头奖的机率差不多。换句话说，要是你觉得“3年内给我一次头奖也不为过吧”，那么在台下咬手帕看别人3年内中了2次头奖，也是很合理的。

  整场年会都给你抽就好了

  比起连年中奖，更令人发指的是在同次年会上连续中奖的家伙，他当自己是五月天领金曲奖吗？

  回到刚刚200人的公司例子里，假设有10项奖品，员工可重复得奖。如此，任何1人抽中2个奖以上的机率是： 1-(10个奖由10个不同的人获得的机率)=1-200×…×191/(200×…×200)=20.4%

  高达1/5的机率，会有位同事跟你说“领奖领得我……脚有点酸”。这并非生而不平等，是每个人都有机会，这次刚好不是你罢了。

  伦敦交易员：重点来了

  不随机的随机

  这种“看起来不大可能，但其实真的如此”的现象生活中俯拾即是，好比随机播放歌曲，如果不把听过的歌从播放清单中移除，10首歌的播放列表，想一次随机顺序（也就是一曲都不重复）的听完10首，只有10!/1010=0.036%，比不可能的任务的机率低，也比汤姆·克鲁斯不离婚的机率低。直接从播放清单移除听过的歌曲可以解决问题，但缺点是1首歌最少得经过10首才能听到第2次。

  据说苹果的随机播放程序是将不同歌手、不同曲风交错播放，让使用者感觉到每一首歌之间毫无关联（用人工干预的不随机来让人感到相当的“随机”）。乔布斯曾说过：“我们减少随机性，藉此让人们感受到多一点的随机(We’re making it less random to make it feel more random)。”

• 好了，准备工作做好了，现在开始正文

  谈谈交易的赌徒模型（具体实践案例可参照马克.沃尔伯格最新出演的电影《赌徒/The Gambler》，但伦敦交易员表示该电影其实不好看）

  交易的时候，随便什么时候猜一个方向，如果错了就反向加倍开仓再来，价格总得回来吧，不可能一路涨不回头（跌不回头）吧，我每次翻倍再来，回来一次我就翻本+赢钱了。

  输1块钱不要紧，下次下注2块钱，如果赢了就赚4元，多了1元，如果再错就下注4元，回来就是8块钱，总投入1+2+4=7，还是赚一元。

  如此这般如意算盘，啥都不需要知道，每回稳赚1元。

  再来！再来！最后总是我赚钱！

  这种经典的赌徒谬误却如同庞氏骗局一般，拥有惊人的生命力，长时间经久不衰，屹立不倒，坑骗着一代又一代的投机客们。

  抛掷硬币出现正面的概率或期望值是0.5，但如果仅抛掷一次，则出现正面的概率是0或1（远远偏离0.5）。随着抛掷次数的增加（即样本的增大），那么硬币出现正面的概率就逐渐接近0.5。但根据认知心理学的“小数定律”，人们通常会忽视样本大小的影响，认为小样本和大样本具有同样的期望值。

  出现了好多次正面之后，大家总会觉得出现反面的概率增加了。

  轮盘赌的赌桌上，在红色连续出现了多次后，永远有大量的赌客选择重注黑色。

  使用这种策略的话，资金曲线也必然是这样的：

  

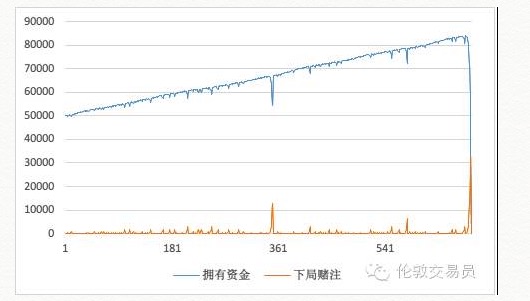
  实践的时候，资金曲线是一路向上的，而且似乎表现得还很稳定。实践到底361次附近的时候，我们可以看到有一次连错，然后坚持该策略的话，不但回本了，而且还继续傲娇得一路向上。

  当然啦，这类策略的最后归宿一定是清零，血本无归。不但血本无归，还会带上美梦破灭的强烈痛苦感。

  笔者见过这样的事情不止一次。每每有人向我宣布一个几乎没有回撤的交易新思路的时候，我就会怀疑，是不是又有人中了赌徒谬误的招了。

  沉迷其中的人，往往不能自拔，所谓的网格交易策略，马丁格尔加仓法，诸如此类的，永远也逃不出赌徒谬误的魔掌，但它必然能获得永生般的生命力。

  因为决定一个策略流行程度的，永远不是它的收益能力，而是他是否契合人性。

  世间上的任何事物，似乎只要符合人性的期望，就会获得顽强的生命力。就如同旁氏骗局一样。网格策略也好，马丁格尔策略也罢，一开始总是给你一个非常非常稳定个的回报 预期。而且没有资金回撤。

  人类的大脑厌恶损失，远甚于收益。（伦敦交易员补一句，这个也是各个对赌的交易商能赚钱的理论支持）这是人类的祖先在远古时期进化而来的策略，因为草原上的祖先们可来不及思考太久远之后的事情，填饱肚子，干完这一餐再说。

  然而，人类的文明飞速发展，日新月异，生物学意义上的大脑，仍然以百万年作为单位进化着。一颗远古的大脑，如何能够面对如今的金融市场呢？故而，千万别凭借自己的主观感受来判断市场，判断策略；需要依赖人类的知识，而非感受。

  （吐血推荐一本神书：Neuroeconomics, Second Edition)）

  各位如果被人推荐了稳赚不赔的交易策略，并且推广者信心满满得认为不需要对市场有任何洞见，以“资金管理”作为主要交易法则。那你要当心了，很有可能是赌徒谬误的另外一个新装。

  金融市场有点类似热力学的系统，大家需要牢记热力学提供的结论，防止上当受骗。

  最重要的是能量守恒定律，能量不会凭空产生，也不会凭空消失。市场上，你不做任何贡献或者洞见的话，也没有使得市场变得更有效的资源的话，不可能凭空产生利润，这是违反自然定律的事情。

  没有任何一种策略可以违反自然规律，这是可以确定的事情。每一种有效的策略，必然是用到了信息不对称的优势，或者拥有超人的洞见能力，或者动用了自己的资源，使得市场更加有效。你得做出相应的贡献，才可能让市场回报你。

  网格交易策略（错了就翻倍加仓），妄图不提供任何输出，就获得收益，就好比想要制造永动机一样，必然是痴人说梦。

  在不考虑交易成本的情况下，网格策略（随便做一个方向，永不止损平仓，一旦对了，立马兑现利润，一旦错了，做反向，仓位翻倍。）的预期收益为零。

  这个预期收益为零仅仅是数学上的，考虑到交易成本的话，预期收益是负的，也就是必亏策略。

  复次，考虑到网格策略说需要追加的投资是符合复利模型的，故而连错几次之后，需要的新投入资金将是天文数字。而不坚持这个局，就会血本无归。

  融资能力，终归是有上限的，因为该约束的存在，不太美妙的下场是必然的。

  道理人人都懂，坚守，却如此艰难。

  但是但是！！！ 说了那么多天上没馅饼，大家看得好失望，我们懂得了赌徒谬误后，来看看什么叫棋高一招的聪明人吧。

  转自人人网上的一位网友的妙文：

  一个怎么看都很“公平”的游戏：一个简单的机械装置，有两个投币口，分别代表黑色与白色。玩家则把相应押注的游戏币投进去（游戏币与一元现金等值）。等到所有玩家投币结束，机器开始运转，并随机从黑白两个小孔中掉出一个球来。输家清空，赢家有一倍奖金。

  S君讲到这里，我意识到这个赌局等于说老板为一个各占1/2的互斥事件都开了1的赔率。这种模型下，无论玩家采用怎样的混合策略，期望收益始终为零。

  我没想出怎样获胜，我也不认为有可能获胜。

  S君接着说，他的策略很简单。即一次选定一种颜色，如黑色。则第一次赌一块钱在黑色；如果输了，第二次压两块钱继续黑色；如果再输，第三次四块钱黑色……如此往复。如果n轮不赢，就在第n+1轮压2的n方于黑色。如果一旦赢了就收手开始下一次一元、两元、四元的新循环。

  这种方法的好处是，无论前面亏了多少钱，只要接下来赢一次，就能扭亏为盈，净赚一元，而n次连续失败的概率非常小，仅为1/(2^n)。

  当然了，这种方法不足以唬到我。当我之前说任何混和策略期望都为零的时候自然也把这种策略包括在内。

  这种策略看起来失手的概率很小，为什么期望还是零呢？很简单，因为他的赌注太大了，假设前7次都输了，那么第八次就不得不压上256元才有可能翻本。但是第八次再输，就累计亏损511元，我不认为身为初中生的S还有资本继续赌下去。换句话说，失败的概率虽小，但每次出现七八次不中的小概率事件时损失也是致命的，足以让他几周之内都没钱继续游戏。再者，这个策略每一个成功的循环只能收益1元，要想获得稳定收益，必须大量重复。以每次循环两次估计，要想赚到20块钱就需要玩40把。四十已经超过了2的五次方32，也就是说，想用这个策略赚20块就几乎肯定会遭遇连续五次白色，以至于亏掉32元。这显然是非常不理智的。

  老实说，我非常怀疑这个策略的可行性。

  行文到这里，我们可以知道，这是个和网格策略一样的简单策略，是赌徒谬误的经典形式。看到这里，我本来以为是另外一个上当的赌徒而已。

  然而事实上，S君确实采用这个策略，每次在游戏机房里赚到20-30个币之后，接着去玩其他游戏逍遥一下午。我并非只是完全相信他的一面之词，而是他后来的分析使我不得不相信这种策略确实是行之有效的，因为我之前的分析犯了致命的错误。

  “汉平，你的致命错误在于……你相信这是一个完全公平的博弈。”

  这里有意思的地方来了，超级干货。（伦敦交易员推荐仔细阅读）

  “什么意思？”

  S君笑着说，“你的分析从数学角度无懈可击。可是别忘了，你的结论是玩家期望为零，换句话说，庄家的期望也是零。可是庄家的收益真的是零吗，如果是零，他买这个机器教这份租金岂不是亏了？”

  事实上S君的想法我也想过，庄家一定会赚钱。唯一的方法就是庄家在操纵小球。做个极端的假设，假如有人赌一万在白色，那么他能获胜的概率就非常小了，庄家不会坐视几周的流水付之东流。虽然不会有人在游戏机房赌上一万，但是据S说，一次赌上200-300的成年土豪并不少见。

  对庄家来说，最贪心的情况莫过于每次都操控小球落在投注较小的颜色上，这样每次都赚。但这样显然不是常态，如果太明显而被玩家意识到，那就无法愉快的玩耍了。

  庄家应该有赢有输，总体上维持一个适当的小收益，比如每十局10%，虽然不大但是比起什么金融理财产品还是堪称暴利了。

  我有些疑惑：“那么对玩家来说，应该每次都站在少数一方，那也不是你这个策略呀。”

  S接着说，这个机器设置是每个玩家走上前投币的。不与玩家交流的话，基本上看不到其他玩家把币投到了那个地方，而每次都与其他玩家交流再做决策又是不可能的。

  我：“所以“少数获胜”这个“潜规则”并没有实际意义？”

  S：“不能这么孤立地看——其实当你意识到这个博弈存在‘潜规则’的时候，就已经比之前前进很多了。我们接下来思考其他的、足以利用的潜规则。”

  我：“还有其他的吗，我觉得少数获胜已经足以让老板赚钱了。”

  S：“老板事先已经承担了机器以及场地的成本，也就是说，他在这次博弈中是负债的。他不仅不能亏欠，还必须要赚钱。而赚钱有两个必要条件，一个是不能让某人一次赚走巨款，这就是所谓少数获胜，但另一个重要的条件是——在稳定收益的前提下吸引尽可能多的玩家。”

  我：“从赌徒的心里来说，这场博弈不用交税，胜负看起来各半，其实已经非常诱人了。”

  S：“但是不具备数学思维的其他玩家并不这么看。我们回到一开始你质疑我的问题，你说我的策略虽然失败的概率不大，但是一旦失败就会损失惨重是吧？”

  我：“对啊，虽然失败的概率只有1/(2^n)，但是一旦失败就会亏损2^n左右——总体期望始终为零。”

  S：“你不妨仔细想想我可能失败的情况。我手里一般有300元左右，足以从压1块开始支撑我到压128元，也就是玩8次。我失败的唯一可能是，连续八次都是白色，那我就完了。”

  我：“虽然可能性很小，但是确实存在……而且损失很大……”

  S：“你错了，这种概率只存在于数学之中。实际上绝无可能——老板不允许这种情况出现。试想在游戏中，一旦出现八次同一颜色，对于我来说，固然可以接受，因为我玩过上千次了，八次白色的概率是1/128，总会遇到的。但是对于其他偶尔只玩过一次的玩家，他们会怎么想，是愿意接受自己就是撞到了1/128的运气，还是开始质疑庄家？何况这游戏庄家本来就在操控。”

  想要让玩家不质疑游戏被操控，不是真的不操控，而是只要让他们不感觉到被操控。

  基于这样的原则，即便是正常分布下的小概率事件也必须拿掉，因为他们会引来质疑（因为公平所以让人感觉不公平）。反而温水煮青蛙式的偶尔操纵几盘少数获胜，因为庄家事先也不知道白色与黑色那个是少数，所以从结果上来看，并不会破坏黑白色的平均分布。

  所以庄家并不顾忌让少数获胜，因为这种诡计并不打破直观上黑白的平衡。但绝对不允许存在的是“连续多次出现同一种颜色”，虽然在大量游戏中理应出现这种小概率事件。

  它们是数学中的小概率事件，却在现实中被修正为零概率事件。

  讲到这里我才完全明白了S真正敏锐的地方，也明白为何这么一个简单的策略可以在这样一个“公平”的博弈中始终获胜了。

  后来S又补充说，他认为老板刻意控制10%的收益太麻烦了，毕竟老板还要照顾其他游戏和玩家。所以更接近事实的推测是，这个机器本身自带了一种随机分布。在这种分布下，老板确实收益和玩家整体一样，都是零。而老板只要每天抽一段时间，操纵几次游戏，使得这几次游戏中老板始终赚到足够钱，其他时间就让机器自动运转。这样除非出现有人压一万这种情况老板如临大敌以外，这个公平的机器就是一个聚宝盆了。

  而S的策略不仅对贪心的老板有效，对看似公平的机器同样也试用。道理很简单，那是一个十几年前的机器，里面固然有电子成分，但更多的还是一个简单的机械装置。其实包括电脑在内，任何人造机器都无法真正地表示出“随机性”，任何程序中的随机数本质上都是一种复杂运算下的伪随机。当然，由于电脑的计算能力非常强大，它产生的随机性非常强，可以模拟数百万种情况。

  但对于简单的机械，模拟数十种情况就需要很大的成本，并且毫无必要——假设这台机器只预存了黑黑黑黑黑、白黑黑黑黑、白白黑黑黑……白白白白白等五次博弈的全部分布，也就是2^5=32种情况，这对于偶尔玩之的玩家来说已经足够随机与公平了——除了S。

  对S而言，如果机器只预存了这32种情况并且反复调用，那么他的策略只要准备五次赌博所必须的1+2+4+8+16=31元就可以始终获胜了。

  事实上S在第一次就提钱买好30多个币。每一次以这些币为资本，赚到额外的20-30个币之后，去玩真正想玩的游戏。也就是说机器预存的情况确实小于等于32钟。

  到这时候，我才发现我与S的思维差距有多么大，我的所有判断都基于数学，而这部分在之前两三百字就解决的“无懈可击”，可是后面的数千字才是S所真正思考的领域。

  笔者第一次看完这段后，如同醍醐灌顶，脱胎换骨！

  毕竟是和人博弈，笔者之前一直陶醉在数字组成的量化世界里，搜索着期望收益更高的策略，而忽略了一个就在眼前，天一般大的基本事实：

  投机交易是在和有血有肉的人在博弈啊！量化永远只是手段和方法，交易者毕竟是在和人做交易啊。所谓的交易，是有一个交易对手和你完成的。投机市场，是和人博弈，不是一个算式。（所以伦敦交易员一直在强调，让机器做机器擅长的，把人擅长的部分留给人自己）

  顿悟到这一点，后面的话便不难理解。

  S说有时候有急事或者其他原因，他来不及把赚的游戏币花光就要回家了。他很少会找老板把剩余的币换成钱（原则上可以）。但是考虑到他要重复使用这个策略，那么事实上就不可以贪图小利而让老板起疑——他会选择一个数学上明显会输的游戏把币迅速输光。当然了，偶尔也会小赚一点——一直到初三那家店忽然倒闭，扣去手上的30多个游戏币，也赚了几十块钱，毕竟主要还是为了开心，不是靠这个发财。

  这就是S的故事。

  高明的S君，必然是能明白老板拥有的信息优势，作为交易对手的赌场老板有权力中止这场游戏，聪明的策略是见好就收。

  唯有更高一层，才能胜过你的对手，唯有不同的洞见，才能获得应有的利润。

  妄图凭空获利，不劳而获，是受骗上当的根本原因。

  这个世界上有没有不判断价格走势的获利策略呢？

  是有的，但它们能够成功是因为它们贡献了，并非不劳而获。

  试简单举一例子，国外的伦敦金也好，纽约金也好，和上海的沪金都是完全拥有一样化学属性的东西。

  但因为两者在不同的交易所内进行交易，故而能产生一种叫“跨市套利”的策略。该策略利用了“一价定律”，也就是说同样的东西，在同样的时刻只可能有一种价格。

  有交易优势的机构，利用自己在IT和资金上的优势，抢先在价格发生偏离的时候，做空高价格的黄金，做多价格比较低的黄金产品。关于IT技术和高频策略的套利方式，请见文章《华尔街猎狼者（高频实战）》

  价格必然回归，则这一组合投资将获利，无须关心黄金未来的涨是跌，就能雯雯得获利。（如果黄金未来上涨，则低价做多的黄金赚钱要多余高价做空的头寸损失，反之亦然）

  因为该机构输出了自己的资源，帮助市场更加有效，从而获得应有的回报。（跨市套利策略是大机构的菜，大家别贸然去介入）

  再再再次告诫大家：天上不会掉馅饼。

  如同伦敦交易员不断反复强调的一样：如果你不知道这笔生意，你的优势在哪里，别人为什么需要你，你的上限在哪里，不对为什么产生利润，清晰透彻。那这笔交易，你别去做。

  没把握的交易，不做，比及时止损还要好。当然如果已经做了交易，有问题了，还是及时止损，这是生存前提。（活着才是硬道理）

• 小总结一下：

  不要相信所谓的赠金和返头寸类的策略能够产生真实的收益，除非你对旁氏骗局的爆发点能有洞见。（就算你很清楚内幕，依然不主张，不鼓励大家去旁氏骗局里火中取栗）

  对于任何高息承诺，心里都要有个疑问在。不搞清楚投资的去向，都应该小心谨慎。

  如同网格类策略一样，没有任何回撤的策略，都要当心一点。为什么能有如此漂亮的业绩，到底是有哪方面的优势？它掌握了什么别人还没掌握的资源或者知识？

  如果没有什么非凡的创见或者资源，那必然是要被市场要回去的。

(本文来源：伦敦交易员）