1. Quadrat
  2. Strategie für den Cyberzyklus von Signal-Gleichungshelfern

Strategie für den Cyberzyklus von Signal-Gleichungshelfern

Schriftsteller:ChaoZhang, Datum: 2024-02-19 10:42:34
Tags:

img

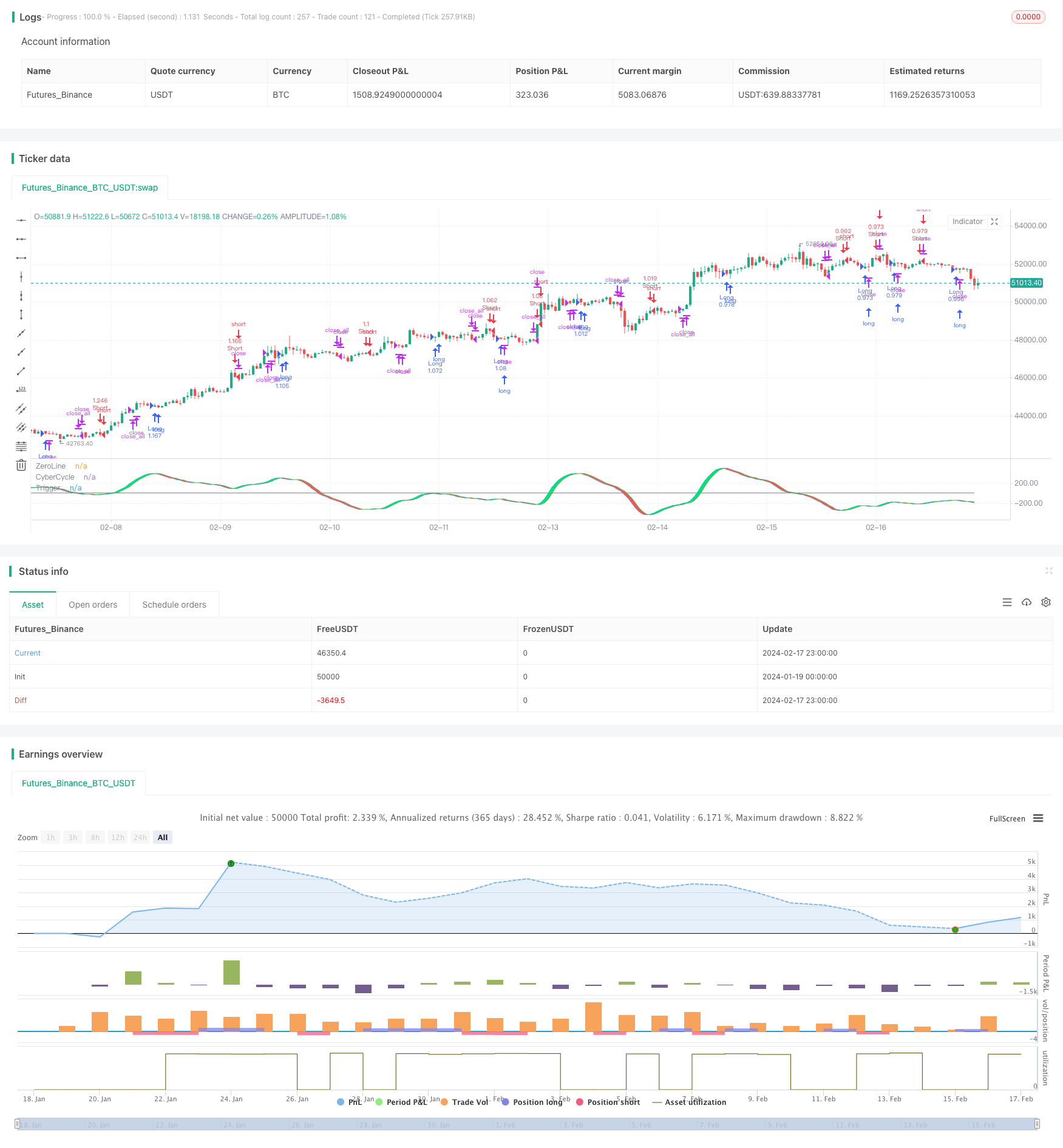
Übersicht

Diese Strategie berechnet das glatte Preissignal auf der Grundlage der von Ehlers vorgeschlagenen Cyberzyklustheorie, um eine Handelsstrategie mit glatten Handelssignalen zu entwickeln.

Strategieprinzip

  1. Das ursprüngliche Preissignal src wird mit einer zweiten Ordnungsgleichung glättet, um das glättete Signal glättend zu erhalten.

  2. Der zyklische Indikatorzyklus wird anhand des glätteten Signals berechnet. Zyklus:= (1 - 0,5alpha) (1 - .5 alpha)(glatt - 2glatt[1] + glatt[2]) + 2(1 - alpha)Zyklus[1] - (1 - alpha)(1-Alpha) * Zyklus [2]

    wobei α der Glättungsparameter ist.

  3. Der zyklische Indikator wird exponentiell mit einer ersten Ordnungsgleichung glättet, um das endgültige Handelssignalsignal zu erhalten. Signal: = alpha2Zyklus + (1 - alpha2)nz ((Signal[1])

    wobei α2 der Glättungsparameter erster Ordnung ist.

  4. Lang, wenn das Signal über das Signal kreuzt[1]; Kurz, wenn das Signal unter dem Signal kreuzt[1].

Analyse der Vorteile

  1. Die zweitrangige Glättung des Preissignals kann Hochfrequenzgeräusche effektiv filtern und Handelssignale zuverlässiger machen.

  2. Durch die Anwendung der Ehlers-Theorie des Cyberzyklus kann der Wendepunkt der Markttrends genauer ermittelt werden.

  3. Die exponentielle Glättung erster Ordnung filtert einen Teil des Rausches im zyklischen Indikator aus, um zuverlässigere Handelssignale zu erzeugen.

  4. Der gesamte Prozess der Strategie ist vernünftig und wissenschaftlich, mit großem Parameteroptimierungsraum und ausgezeichneter tatsächlicher Leistung.

Risikoanalyse

  1. Wie andere Strategien für technische Indikatoren ist auch diese relativ anfällig für systemische Marktrisiken und kann im Falle von Schwarzen Schwanen große Verluste verursachen.

  2. Aufgrund des komplexen Berechnungsvorgangs können unsachgemäße Parametereinstellungen zu Berechnungsverzögerungen führen und dadurch die tatsächliche Leistung beeinträchtigen.

  3. Die Ausgleichenverarbeitung führt auch zu verzögerten Handelssignalen, die möglicherweise keine Marktturnpunkte rechtzeitig erfassen und somit Chancen verpassen.

Optimierungsrichtlinien

  1. Es können verschiedene Arten von Glättungsalgorithmen getestet werden, z. B. eine exponentielle Glättung erster Ordnung, eine gleitende Durchschnittsglättung usw., um das optimale Glättungsschema zu finden.

  2. Es kann ein adaptives Parameter-Tuning-Mechanismus eingeführt werden, um die Parameter dynamisch anhand der Marktbedingungen anzupassen, um die Strategiezuverlässigkeit zu verbessern.

  3. Stop-Loss- und Take-Profit-Strategien können so konzipiert werden, dass das Risiko eines einzelnen Verlusts reduziert und gleichzeitig Gewinne erzielt werden.

  4. Es kann mit anderen Modellen des maschinellen Lernens kombiniert werden, um Modellportfolios zu erstellen und andere Modelle zur Filterung von Handelssignalen zu verwenden.

Zusammenfassung

Diese Strategie entwirft eine Handelssignal-Gleichung Ehlers Cyber-Zyklus-Handelsstrategie durch Preissignal-Gleichung und Ehlers Cyber-Zyklus-Indikator-Berechnung. Es kann effektiv Filterlärm und erzeugen zuverlässigere Handelssignale. Gleichzeitig ist der Parameter-Raum groß und die tatsächliche Leistung ist gut. Durch die Einführung von adaptiven Mechanismen, Stop-Loss-Strategien und otras-Optimierung kann die Stabilität und Effektivität der Strategie weiter verbessert werden.

/*backtest
start: 2024-01-19 00:00:00
end: 2024-02-18 00:00:00
period: 1h
basePeriod: 15m
exchanges: [{"eid":"Futures_Binance","currency":"BTC_USDT"}]
*/

//@version=3
strategy("Ehlers Cyber Cycle Strategy",overlay=false, default_qty_type = strategy.percent_of_equity, default_qty_value = 100.0, pyramiding = 1, commission_type = strategy.commission.percent, commission_value = 0.1)
src = input(hl2, title = "Source") 
alpha = input(.07, title = "Alpha")
lag = input(9, title = "Lag")
smooth = (src + 2 * src[1] + 2 * src[2] + src[3]) / 6

cycle = na
if na(cycle[7])
    cycle := (src - 2 * src[1] + src[2]) / 4
else
    cycle := (1 - .5 * alpha) * (1 - .5 * alpha) * (smooth - 2 * smooth[1] + smooth[2]) + 2 * (1 - alpha) * cycle[1] - (1 - alpha) * (1 - alpha) * cycle[2]

alpha2 = 1 / (lag + 1)
signal = na
signal := alpha2 * cycle + (1 - alpha2) * nz(signal[1])
oppositeTrade = input(true)
barsSinceEntry = 0
barsSinceEntry := nz(barsSinceEntry[1]) + 1
if strategy.position_size == 0
    barsSinceEntry := 0
if (crossover(signal, signal[1]) and not oppositeTrade) or (oppositeTrade and crossunder(signal, signal[1]))
    strategy.entry("Long", strategy.long)
    barsSinceEntry := 0
if (crossunder(signal, signal[1]) and not oppositeTrade) or (oppositeTrade and crossover(signal, signal[1]))
    strategy.entry("Short", strategy.short)
    barsSinceEntry := 0
if strategy.openprofit < 0 and barsSinceEntry > 8
    strategy.close_all()
    barsSinceEntry := 0
    
    
plot(0, title="ZeroLine", color=gray) 
plotSrc = signal
cyclePlot = plot(plotSrc, title = "CyberCycle", color = blue)
triggerPlot = plot(plotSrc[1], title = "Trigger", color = green)
fill(cyclePlot, triggerPlot, color = plotSrc < plotSrc[1] ? red : lime, transp = 50)
Mehr

2019 FMZ - Alle Rechte vorbehalten