The resource loading... loading...
  1. Square
  2. Gaussian Channel Trend Following Strategy

Gaussian Channel Trend Following Strategy

Author: ChaoZhang, Date: 2024-03-29 16:26:26
Tags:

img

Overview

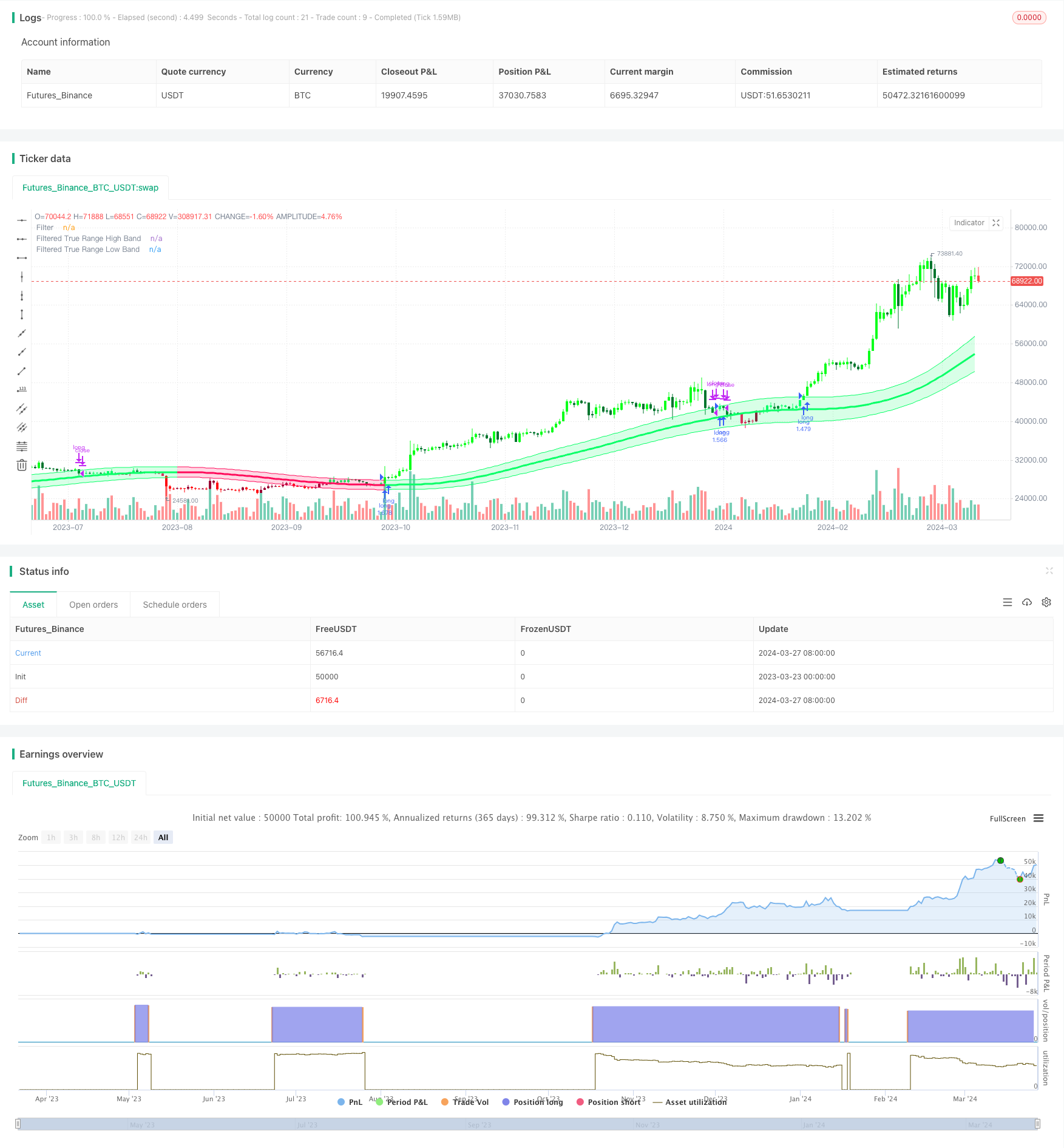
The Gaussian Channel Trend Following Strategy is a trend-following trading strategy based on the Gaussian Channel indicator. The strategy aims to capture the main trends in the market, buying and holding positions during uptrends and closing positions during downtrends. It uses the Gaussian Channel indicator to identify the direction and strength of the trend by analyzing the relationship between price and the upper and lower bands of the channel. The main goal of the strategy is to maximize profits during sustained trends while minimizing trading frequency during range-bound markets.

Strategy Principle

The core of the Gaussian Channel Trend Following Strategy is the Gaussian Channel indicator, which was proposed by Ehlers. It combines Gaussian filtering techniques with True Range to analyze trend activity. The indicator first calculates beta and alpha values based on the sampling period and number of poles, then applies a filter to the data to obtain a smoothed curve (midline). Next, the strategy multiplies the smoothed True Range by a multiplier to generate the upper and lower channels. When the price crosses above/below the upper/lower channel, it generates a buy/sell signal. Additionally, the strategy offers features to reduce indicator lag and a fast response mode.

Strategy Advantages

  1. Trend Following: The strategy excels at capturing the main trends in the market, investing in the direction of the trend, which helps to achieve long-term stable returns.
  2. Reduced Trading Frequency: The strategy only enters positions when a trend is confirmed and maintains positions during the trend, thus reducing unnecessary trading and transaction costs.
  3. Lag Reduction: Through the reduced lag mode and fast response mode, the strategy can react more promptly to market changes.
  4. Flexible Parameters: Users can adjust strategy parameters according to their needs, such as sampling period, number of poles, True Range multiplier, etc., to optimize strategy performance.

Strategy Risks

  1. Parameter Optimization Risk: Improper parameter settings may lead to poor strategy performance. It is recommended to perform parameter optimization and backtesting in different market environments to find the optimal parameter combination.
  2. Trend Reversal Risk: When market trends suddenly reverse, the strategy may experience significant drawdowns. This can be mitigated by setting stop-losses or introducing other indicators to control risk.
  3. Range-bound Market Risk: In range-bound markets, the strategy may generate frequent trading signals, leading to diminished returns. This can be addressed by optimizing parameters or combining with other technical indicators to filter signals.

Strategy Optimization Directions

  1. Incorporate Other Technical Indicators: Combine with other trend-following or oscillator indicators, such as MACD, RSI, etc., to improve signal accuracy and reliability.
  2. Dynamic Parameter Optimization: Dynamically adjust strategy parameters based on changes in market conditions to adapt to different market environments.
  3. Add Risk Control Module: Set reasonable stop-loss and take-profit rules to control individual trade risk and overall drawdown levels.
  4. Multi-Timeframe Analysis: Combine signals from different time frames, such as daily and 4-hour charts, to obtain more comprehensive market information.

Summary

The Gaussian Channel Trend Following Strategy is a trend-following trading strategy based on Gaussian filtering techniques, which aims to capture the main market trends for long-term stable returns. The strategy uses the Gaussian Channel indicator to identify trend direction and strength while offering features to reduce lag and provide fast response. The advantages of the strategy lie in its strong trend-following ability and low trading frequency. However, it also faces risks such as parameter optimization, trend reversals, and range-bound markets. Future optimizations can include incorporating other technical indicators, dynamic parameter optimization, adding risk control modules, and multi-timeframe analysis to further improve the strategy’s robustness and profitability.

/*backtest
start: 2023-03-23 00:00:00
end: 2024-03-28 00:00:00
period: 1d
basePeriod: 1h
exchanges: [{"eid":"Futures_Binance","currency":"BTC_USDT"}]
*/

//@version=5
strategy(title="Gaussian Channel Strategy v2.0", overlay=true, calc_on_every_tick=false, initial_capital=1000, default_qty_type=strategy.percent_of_equity, default_qty_value=100, commission_type=strategy.commission.percent, commission_value=0.1, slippage=3)

//-----------------------------------------------------------------------------------------------------------------------------------------------------------------
// Gaussian Channel Indicaor - courtesy of @DonovanWall
//----------------------------------------------------------------------------------------------------------------------------------------------------------------- 

// Date condition inputs
startDate = input(timestamp("1 January 2018 00:00 +0000"), "Date Start", group="Main Algo Settings")
endDate = input(timestamp("1 January 2060 00:00 +0000"), "Date Start", group="Main Algo Settings")
timeCondition = true

// This study is an experiment utilizing the Ehlers Gaussian Filter technique combined with lag reduction techniques and true range to analyze trend activity.
// Gaussian filters, as Ehlers explains it, are simply exponential moving averages applied multiple times.
// First, beta and alpha are calculated based on the sampling period and number of poles specified. The maximum number of poles available in this script is 9.
// Next, the data being analyzed is given a truncation option for reduced lag, which can be enabled with "Reduced Lag Mode".
// Then the alpha and source values are used to calculate the filter and filtered true range of the dataset.
// Filtered true range with a specified multiplier is then added to and subtracted from the filter, generating a channel.
// Lastly, a one pole filter with a N pole alpha is averaged with the filter to generate a faster filter, which can be enabled with "Fast Response Mode". 

// Custom bar colors are included.

// Note: Both the sampling period and number of poles directly affect how much lag the indicator has, and how smooth the output is.
//      Larger inputs will result in smoother outputs with increased lag, and smaller inputs will have noisier outputs with reduced lag.
//      For the best results, I recommend not setting the sampling period any lower than the number of poles + 1. Going lower truncates the equation.

//-----------------------------------------------------------------------------------------------------------------------------------------------------------------
// Updates:
// Huge shoutout to @e2e4mfck for taking the time to improve the calculation method!
// -> migrated to v4
// -> pi is now calculated using trig identities rather than being explicitly defined.
// -> The filter calculations are now organized into functions rather than being individually defined.
// -> Revamped color scheme.

//-----------------------------------------------------------------------------------------------------------------------------------------------------------------
// Functions - courtesy of @e2e4mfck
//----------------------------------------------------------------------------------------------------------------------------------------------------------------- 

// Filter function 
f_filt9x (_a, _s, _i) => 
    int _m2 = 0, int _m3 = 0, int _m4 = 0, int _m5 = 0, int _m6 = 0, 
    int _m7 = 0, int _m8 = 0, int _m9 = 0, float _f = .0, _x = (1 - _a)
    // Weights. 
    // Initial weight _m1 is a pole number and equal to _i
    _m2 := _i == 9 ? 36  : _i == 8 ? 28 : _i == 7 ? 21 : _i == 6 ? 15 : _i == 5 ? 10 : _i == 4 ? 6 : _i == 3 ? 3 : _i == 2 ? 1 : 0
    _m3 := _i == 9 ? 84  : _i == 8 ? 56 : _i == 7 ? 35 : _i == 6 ? 20 : _i == 5 ? 10 : _i == 4 ? 4 : _i == 3 ? 1 : 0
    _m4 := _i == 9 ? 126 : _i == 8 ? 70 : _i == 7 ? 35 : _i == 6 ? 15 : _i == 5 ? 5  : _i == 4 ? 1 : 0
    _m5 := _i == 9 ? 126 : _i == 8 ? 56 : _i == 7 ? 21 : _i == 6 ? 6  : _i == 5 ? 1  : 0 
    _m6 := _i == 9 ? 84  : _i == 8 ? 28 : _i == 7 ? 7  : _i == 6 ? 1  : 0 
    _m7 := _i == 9 ? 36  : _i == 8 ? 8  : _i == 7 ? 1  : 0 
    _m8 := _i == 9 ? 9   : _i == 8 ? 1  : 0 
    _m9 := _i == 9 ? 1   : 0
    // filter
    _f :=   math.pow(_a, _i) * nz(_s) + 
      _i  *     _x      * nz(_f[1])      - (_i >= 2 ? 
      _m2 * math.pow(_x, 2)  * nz(_f[2]) : 0) + (_i >= 3 ? 
      _m3 * math.pow(_x, 3)  * nz(_f[3]) : 0) - (_i >= 4 ? 
      _m4 * math.pow(_x, 4)  * nz(_f[4]) : 0) + (_i >= 5 ? 
      _m5 * math.pow(_x, 5)  * nz(_f[5]) : 0) - (_i >= 6 ? 
      _m6 * math.pow(_x, 6)  * nz(_f[6]) : 0) + (_i >= 7 ? 
      _m7 * math.pow(_x, 7)  * nz(_f[7]) : 0) - (_i >= 8 ? 
      _m8 * math.pow(_x, 8)  * nz(_f[8]) : 0) + (_i == 9 ? 
      _m9 * math.pow(_x, 9)  * nz(_f[9]) : 0)

// 9 var declaration fun
f_pole (_a, _s, _i) =>
    _f1 =            f_filt9x(_a, _s, 1),      _f2 = (_i >= 2 ? f_filt9x(_a, _s, 2) : 0), _f3 = (_i >= 3 ? f_filt9x(_a, _s, 3) : 0)
    _f4 = (_i >= 4 ? f_filt9x(_a, _s, 4) : 0), _f5 = (_i >= 5 ? f_filt9x(_a, _s, 5) : 0), _f6 = (_i >= 6 ? f_filt9x(_a, _s, 6) : 0)
    _f7 = (_i >= 2 ? f_filt9x(_a, _s, 7) : 0), _f8 = (_i >= 8 ? f_filt9x(_a, _s, 8) : 0), _f9 = (_i == 9 ? f_filt9x(_a, _s, 9) : 0)
    _fn = _i == 1 ? _f1 : _i == 2 ? _f2 : _i == 3 ? _f3 :
      _i == 4     ? _f4 : _i == 5 ? _f5 : _i == 6 ? _f6 :
      _i == 7     ? _f7 : _i == 8 ? _f8 : _i == 9 ? _f9 : na
    [_fn, _f1]

//-----------------------------------------------------------------------------------------------------------------------------------------------------------------
// Inputs
//-----------------------------------------------------------------------------------------------------------------------------------------------------------------

// Source
src = input(defval=hlc3, title="Source")

// Poles
int N = input.int(defval=4, title="Poles", minval=1, maxval=9)

// Period
int per = input.int(defval=144, title="Sampling Period", minval=2)

// True Range Multiplier
float mult = input.float(defval=1.414, title="Filtered True Range Multiplier", minval=0)

// Lag Reduction
bool modeLag  = input.bool(defval=false, title="Reduced Lag Mode")
bool modeFast = input.bool(defval=false, title="Fast Response Mode")

//-----------------------------------------------------------------------------------------------------------------------------------------------------------------
// Definitions
//-----------------------------------------------------------------------------------------------------------------------------------------------------------------

// Beta and Alpha Components
beta  = (1 - math.cos(4*math.asin(1)/per)) / (math.pow(1.414, 2/N) - 1)
alpha = - beta + math.sqrt(math.pow(beta, 2) + 2*beta)

// Lag
lag = (per - 1)/(2*N)

// Data
srcdata = modeLag ? src + (src - src[lag]) : src
trdata  = modeLag ? ta.tr(true) + (ta.tr(true) - ta.tr(true)[lag]) : ta.tr(true)

// Filtered Values
[filtn, filt1]     = f_pole(alpha, srcdata, N)
[filtntr, filt1tr] = f_pole(alpha, trdata,  N)

// Lag Reduction
filt   = modeFast ? (filtn + filt1)/2 : filtn
filttr = modeFast ? (filtntr + filt1tr)/2 : filtntr

// Bands
hband = filt + filttr*mult
lband = filt - filttr*mult

// Colors
color1   = #0aff68
color2   = #00752d
color3   = #ff0a5a
color4   = #990032
fcolor   = filt > filt[1] ? #0aff68 : filt < filt[1] ? #ff0a5a : #cccccc
barcolor = (src > src[1]) and (src > filt) and (src < hband) ? #0aff68 : (src > src[1]) and (src >= hband) ? #0aff1b : (src <= src[1]) and (src > filt) ? #00752d : 
           (src < src[1]) and (src < filt) and (src > lband) ? #ff0a5a : (src < src[1]) and (src <= lband) ? #ff0a11 : (src >= src[1]) and (src < filt) ? #990032 : #cccccc

//-----------------------------------------------------------------------------------------------------------------------------------------------------------------
// Outputs
//-----------------------------------------------------------------------------------------------------------------------------------------------------------------

// Filter Plot
filtplot = plot(filt, title="Filter", color=fcolor, linewidth=3)

// Band Plots
hbandplot = plot(hband, title="Filtered True Range High Band", color=fcolor)
lbandplot = plot(lband, title="Filtered True Range Low Band", color=fcolor)

// Channel Fill
fill(hbandplot, lbandplot, title="Channel Fill", color=color.new(fcolor, 80))

// Bar Color
barcolor(barcolor)

longCondition = ta.crossover(close, hband) and timeCondition
closeAllCondition = ta.crossunder(close, hband) and timeCondition

if longCondition
    strategy.entry("long", strategy.long)

if closeAllCondition
    strategy.close("long")
More

2019 FMZ - All rights reserved