Tendencia del canal de Gauss siguiendo la estrategia

El autor:¿ Qué pasa?, Fecha: 2024-03-29 16:26:26
Las etiquetas:

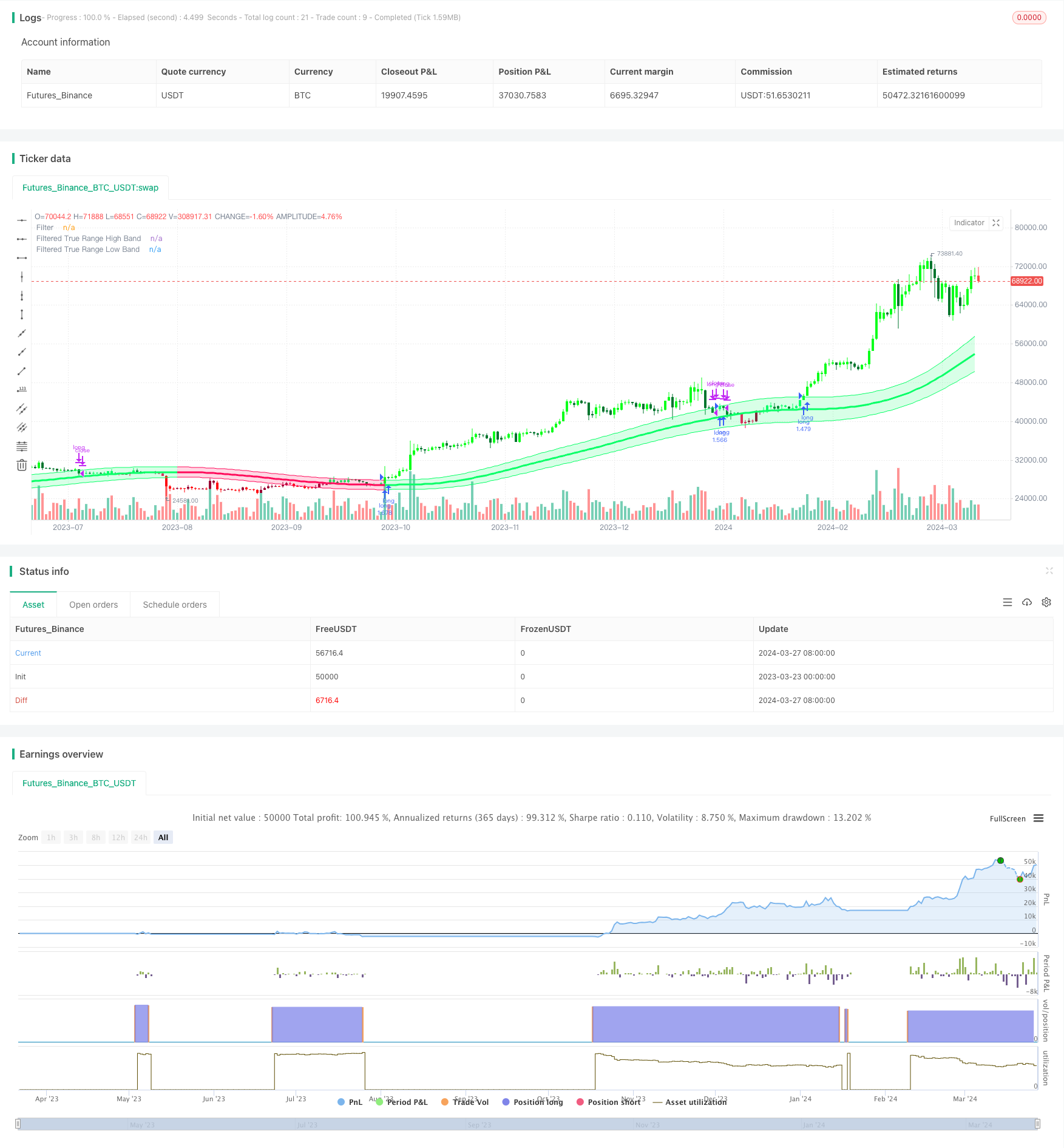
Resumen general

La estrategia de seguimiento de tendencias del canal de Gauss es una estrategia de seguimiento de tendencias basada en el indicador del canal de Gauss. La estrategia tiene como objetivo capturar las principales tendencias en el mercado, comprando y manteniendo posiciones durante las tendencias alcistas y cerrando posiciones durante las tendencias bajistas. Utiliza el indicador del canal de Gauss para identificar la dirección y la fuerza de la tendencia mediante el análisis de la relación entre el precio y las bandas superior e inferior del canal. El objetivo principal de la estrategia es maximizar las ganancias durante las tendencias sostenidas al tiempo que se minimiza la frecuencia durante los mercados de trading de rango.

Principio de la estrategia

El núcleo de la estrategia de seguimiento de tendencia del canal de Gauss es el indicador del canal de Gauss, que fue propuesto por Ehlers. Combina técnicas de filtrado de Gauss con el rango verdadero para analizar la actividad de la tendencia. El indicador primero calcula los valores beta y alfa basados en el período de muestreo y el número de polos, luego aplica un filtro a los datos para obtener una curva suavizada (línea media). A continuación, la estrategia multiplica el rango verdadero suavizado por un multiplicador para generar los canales superior e inferior. Cuando el precio cruza por encima / por debajo del canal superior / inferior, genera una señal de compra / venta. Además, la estrategia ofrece características para reducir el retraso del indicador y un modo de respuesta rápida.

Ventajas estratégicas

Seguimiento de tendencias: La estrategia se destaca por capturar las principales tendencias del mercado, invirtiendo en la dirección de la tendencia, lo que ayuda a lograr rendimientos estables a largo plazo.
Reducción de la frecuencia de negociación: la estrategia solo entra en posiciones cuando se confirma una tendencia y mantiene posiciones durante la tendencia, reduciendo así los costos innecesarios de negociación y transacción.
Reducción del retraso: A través del modo de retraso reducido y el modo de respuesta rápida, la estrategia puede reaccionar más rápidamente a los cambios del mercado.
Parámetros flexibles: Los usuarios pueden ajustar los parámetros de la estrategia de acuerdo con sus necesidades, como el período de muestreo, el número de polos, el multiplicador de rango verdadero, etc., para optimizar el rendimiento de la estrategia.

Riesgos estratégicos

Riesgo de optimización de parámetros: la configuración incorrecta de parámetros puede conducir a un mal rendimiento de la estrategia. Se recomienda realizar optimización de parámetros y pruebas de retroceso en diferentes entornos de mercado para encontrar la combinación óptima de parámetros.
Riesgo de reversión de tendencia: cuando las tendencias del mercado se invierten repentinamente, la estrategia puede experimentar reducciones significativas. Esto puede mitigarse estableciendo stop-loss o introduciendo otros indicadores para controlar el riesgo.
Riesgo de mercado limitado al rango: en los mercados de rango limitado, la estrategia puede generar señales comerciales frecuentes, lo que conduce a una disminución de los rendimientos.

Direcciones para la optimización de la estrategia

Incorporar otros indicadores técnicos: Combinar con otros indicadores de tendencia o osciladores, como el MACD, el RSI, etc., para mejorar la precisión y la fiabilidad de la señal.
Optimización de parámetros dinámicos: ajustar dinámicamente los parámetros de la estrategia en función de los cambios en las condiciones del mercado para adaptarse a los diferentes entornos del mercado.
Añadir un módulo de control de riesgos: establecer normas razonables de stop loss y take profit para controlar el riesgo comercial individual y los niveles generales de extracción.
Análisis de marcos de tiempo múltiples: Combinar señales de diferentes marcos de tiempo, como gráficos diarios y de 4 horas, para obtener información de mercado más completa.

Resumen de las actividades

La estrategia de seguimiento de tendencias del canal de Gauss es una estrategia de seguimiento de tendencias basada en técnicas de filtrado de Gauss, que tiene como objetivo capturar las principales tendencias del mercado para obtener rendimientos estables a largo plazo. La estrategia utiliza el indicador del canal de Gauss para identificar la dirección y la fuerza de la tendencia, al tiempo que ofrece características para reducir el retraso y proporcionar una respuesta rápida. Las ventajas de la estrategia se encuentran en su fuerte capacidad de seguimiento de tendencias y baja frecuencia de negociación. Sin embargo, también enfrenta riesgos como optimización de parámetros, inversiones de tendencia y mercados de rango. Las optimizaciones futuras pueden incluir la incorporación de otros indicadores técnicos, optimización de parámetros dinámicos, adición de módulos de control de riesgos y análisis de marcos de tiempo múltiples para mejorar aún más la robustez y rentabilidad de la estrategia.

/*backtest
start: 2023-03-23 00:00:00
end: 2024-03-28 00:00:00
period: 1d
basePeriod: 1h
exchanges: [{"eid":"Futures_Binance","currency":"BTC_USDT"}]
*/

//@version=5
strategy(title="Gaussian Channel Strategy v2.0", overlay=true, calc_on_every_tick=false, initial_capital=1000, default_qty_type=strategy.percent_of_equity, default_qty_value=100, commission_type=strategy.commission.percent, commission_value=0.1, slippage=3)

//-----------------------------------------------------------------------------------------------------------------------------------------------------------------
// Gaussian Channel Indicaor - courtesy of @DonovanWall
//----------------------------------------------------------------------------------------------------------------------------------------------------------------- 

// Date condition inputs
startDate = input(timestamp("1 January 2018 00:00 +0000"), "Date Start", group="Main Algo Settings")
endDate = input(timestamp("1 January 2060 00:00 +0000"), "Date Start", group="Main Algo Settings")
timeCondition = true

// This study is an experiment utilizing the Ehlers Gaussian Filter technique combined with lag reduction techniques and true range to analyze trend activity.
// Gaussian filters, as Ehlers explains it, are simply exponential moving averages applied multiple times.
// First, beta and alpha are calculated based on the sampling period and number of poles specified. The maximum number of poles available in this script is 9.
// Next, the data being analyzed is given a truncation option for reduced lag, which can be enabled with "Reduced Lag Mode".
// Then the alpha and source values are used to calculate the filter and filtered true range of the dataset.
// Filtered true range with a specified multiplier is then added to and subtracted from the filter, generating a channel.
// Lastly, a one pole filter with a N pole alpha is averaged with the filter to generate a faster filter, which can be enabled with "Fast Response Mode". 

// Custom bar colors are included.

// Note: Both the sampling period and number of poles directly affect how much lag the indicator has, and how smooth the output is.
//      Larger inputs will result in smoother outputs with increased lag, and smaller inputs will have noisier outputs with reduced lag.
//      For the best results, I recommend not setting the sampling period any lower than the number of poles + 1. Going lower truncates the equation.

//-----------------------------------------------------------------------------------------------------------------------------------------------------------------
// Updates:
// Huge shoutout to @e2e4mfck for taking the time to improve the calculation method!
// -> migrated to v4
// -> pi is now calculated using trig identities rather than being explicitly defined.
// -> The filter calculations are now organized into functions rather than being individually defined.
// -> Revamped color scheme.

//-----------------------------------------------------------------------------------------------------------------------------------------------------------------
// Functions - courtesy of @e2e4mfck
//----------------------------------------------------------------------------------------------------------------------------------------------------------------- 

// Filter function 
f_filt9x (_a, _s, _i) => 
    int _m2 = 0, int _m3 = 0, int _m4 = 0, int _m5 = 0, int _m6 = 0, 
    int _m7 = 0, int _m8 = 0, int _m9 = 0, float _f = .0, _x = (1 - _a)
    // Weights. 
    // Initial weight _m1 is a pole number and equal to _i
    _m2 := _i == 9 ? 36  : _i == 8 ? 28 : _i == 7 ? 21 : _i == 6 ? 15 : _i == 5 ? 10 : _i == 4 ? 6 : _i == 3 ? 3 : _i == 2 ? 1 : 0
    _m3 := _i == 9 ? 84  : _i == 8 ? 56 : _i == 7 ? 35 : _i == 6 ? 20 : _i == 5 ? 10 : _i == 4 ? 4 : _i == 3 ? 1 : 0
    _m4 := _i == 9 ? 126 : _i == 8 ? 70 : _i == 7 ? 35 : _i == 6 ? 15 : _i == 5 ? 5  : _i == 4 ? 1 : 0
    _m5 := _i == 9 ? 126 : _i == 8 ? 56 : _i == 7 ? 21 : _i == 6 ? 6  : _i == 5 ? 1  : 0 
    _m6 := _i == 9 ? 84  : _i == 8 ? 28 : _i == 7 ? 7  : _i == 6 ? 1  : 0 
    _m7 := _i == 9 ? 36  : _i == 8 ? 8  : _i == 7 ? 1  : 0 
    _m8 := _i == 9 ? 9   : _i == 8 ? 1  : 0 
    _m9 := _i == 9 ? 1   : 0
    // filter
    _f :=   math.pow(_a, _i) * nz(_s) + 
      _i  *     _x      * nz(_f[1])      - (_i >= 2 ? 
      _m2 * math.pow(_x, 2)  * nz(_f[2]) : 0) + (_i >= 3 ? 
      _m3 * math.pow(_x, 3)  * nz(_f[3]) : 0) - (_i >= 4 ? 
      _m4 * math.pow(_x, 4)  * nz(_f[4]) : 0) + (_i >= 5 ? 
      _m5 * math.pow(_x, 5)  * nz(_f[5]) : 0) - (_i >= 6 ? 
      _m6 * math.pow(_x, 6)  * nz(_f[6]) : 0) + (_i >= 7 ? 
      _m7 * math.pow(_x, 7)  * nz(_f[7]) : 0) - (_i >= 8 ? 
      _m8 * math.pow(_x, 8)  * nz(_f[8]) : 0) + (_i == 9 ? 
      _m9 * math.pow(_x, 9)  * nz(_f[9]) : 0)

// 9 var declaration fun
f_pole (_a, _s, _i) =>
    _f1 =            f_filt9x(_a, _s, 1),      _f2 = (_i >= 2 ? f_filt9x(_a, _s, 2) : 0), _f3 = (_i >= 3 ? f_filt9x(_a, _s, 3) : 0)
    _f4 = (_i >= 4 ? f_filt9x(_a, _s, 4) : 0), _f5 = (_i >= 5 ? f_filt9x(_a, _s, 5) : 0), _f6 = (_i >= 6 ? f_filt9x(_a, _s, 6) : 0)
    _f7 = (_i >= 2 ? f_filt9x(_a, _s, 7) : 0), _f8 = (_i >= 8 ? f_filt9x(_a, _s, 8) : 0), _f9 = (_i == 9 ? f_filt9x(_a, _s, 9) : 0)
    _fn = _i == 1 ? _f1 : _i == 2 ? _f2 : _i == 3 ? _f3 :
      _i == 4     ? _f4 : _i == 5 ? _f5 : _i == 6 ? _f6 :
      _i == 7     ? _f7 : _i == 8 ? _f8 : _i == 9 ? _f9 : na
    [_fn, _f1]

//-----------------------------------------------------------------------------------------------------------------------------------------------------------------
// Inputs
//-----------------------------------------------------------------------------------------------------------------------------------------------------------------

// Source
src = input(defval=hlc3, title="Source")

// Poles
int N = input.int(defval=4, title="Poles", minval=1, maxval=9)

// Period
int per = input.int(defval=144, title="Sampling Period", minval=2)

// True Range Multiplier
float mult = input.float(defval=1.414, title="Filtered True Range Multiplier", minval=0)

// Lag Reduction
bool modeLag  = input.bool(defval=false, title="Reduced Lag Mode")
bool modeFast = input.bool(defval=false, title="Fast Response Mode")

//-----------------------------------------------------------------------------------------------------------------------------------------------------------------
// Definitions
//-----------------------------------------------------------------------------------------------------------------------------------------------------------------

// Beta and Alpha Components
beta  = (1 - math.cos(4*math.asin(1)/per)) / (math.pow(1.414, 2/N) - 1)
alpha = - beta + math.sqrt(math.pow(beta, 2) + 2*beta)

// Lag
lag = (per - 1)/(2*N)

// Data
srcdata = modeLag ? src + (src - src[lag]) : src
trdata  = modeLag ? ta.tr(true) + (ta.tr(true) - ta.tr(true)[lag]) : ta.tr(true)

// Filtered Values
[filtn, filt1]     = f_pole(alpha, srcdata, N)
[filtntr, filt1tr] = f_pole(alpha, trdata,  N)

// Lag Reduction
filt   = modeFast ? (filtn + filt1)/2 : filtn
filttr = modeFast ? (filtntr + filt1tr)/2 : filtntr

// Bands
hband = filt + filttr*mult
lband = filt - filttr*mult

// Colors
color1   = #0aff68
color2   = #00752d
color3   = #ff0a5a
color4   = #990032
fcolor   = filt > filt[1] ? #0aff68 : filt < filt[1] ? #ff0a5a : #cccccc
barcolor = (src > src[1]) and (src > filt) and (src < hband) ? #0aff68 : (src > src[1]) and (src >= hband) ? #0aff1b : (src <= src[1]) and (src > filt) ? #00752d : 
           (src < src[1]) and (src < filt) and (src > lband) ? #ff0a5a : (src < src[1]) and (src <= lband) ? #ff0a11 : (src >= src[1]) and (src < filt) ? #990032 : #cccccc

//-----------------------------------------------------------------------------------------------------------------------------------------------------------------
// Outputs
//-----------------------------------------------------------------------------------------------------------------------------------------------------------------

// Filter Plot
filtplot = plot(filt, title="Filter", color=fcolor, linewidth=3)

// Band Plots
hbandplot = plot(hband, title="Filtered True Range High Band", color=fcolor)
lbandplot = plot(lband, title="Filtered True Range Low Band", color=fcolor)

// Channel Fill
fill(hbandplot, lbandplot, title="Channel Fill", color=color.new(fcolor, 80))

// Bar Color
barcolor(barcolor)

longCondition = ta.crossover(close, hband) and timeCondition
closeAllCondition = ta.crossunder(close, hband) and timeCondition

if longCondition
    strategy.entry("long", strategy.long)

if closeAllCondition
    strategy.close("long")

Más.