Estratégia de negociação quantitativa de estado de transição da cadeia de probabilidade de Markov

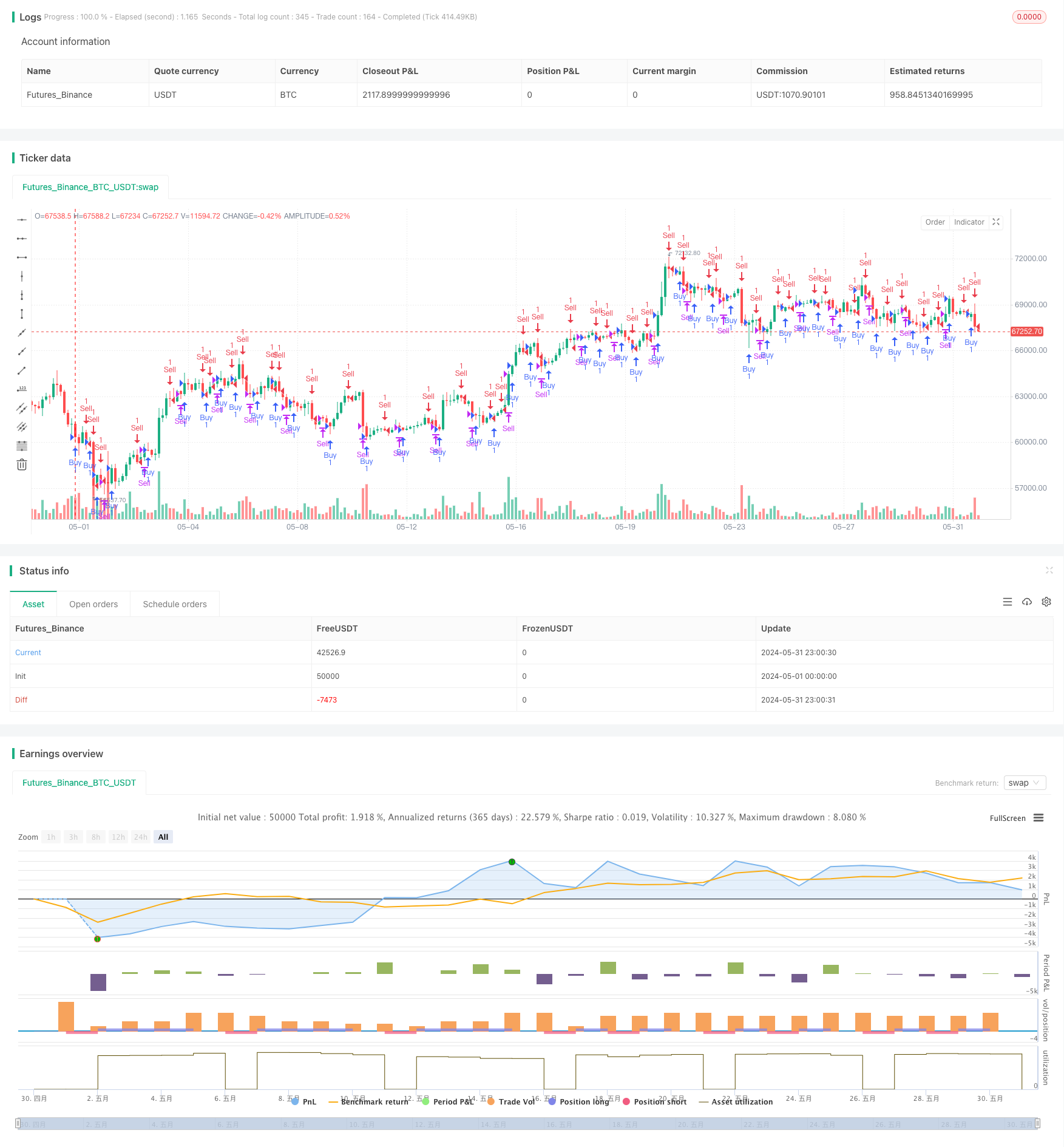
Resumo

A estratégia de negociação quantitativa de estado de transição da cadeia de probabilidade de Markov é uma abordagem de negociação inovadora baseada no modelo da cadeia de Markov. Esta estratégia utiliza as probabilidades de transição de estado de uma cadeia de Markov para prever as tendências do mercado e tomar decisões de negociação em conformidade. A ideia central é dividir os estados do mercado em vários estados discretos (como otimista, de baixa e estagnado), e, em seguida, calcular as probabilidades de transição entre esses estados com base em dados históricos para prever o próximo estado provável do mercado.

A singularidade deste método reside na consideração não só do estado atual do mercado, mas também da dinâmica das transições entre os estados do mercado.

Princípios de estratégia

1. Definição de estado: A estratégia define três estados de mercado - de alta (tendência ascendente), baixa (tendência descendente) e estagnada (estável). Estes estados são determinados comparando o preço de fechamento atual com o preço de fechamento anterior.

2. Probabilidades de transição: a estratégia usa nove parâmetros de entrada para definir as probabilidades de transição entre diferentes estados.prob_bull_to_bullrepresenta a probabilidade de permanecer em um estado de alta dado que o estado atual é de alta.

3. A estratégia utiliza uma lógica de transição simplificada para simular o processo de transição de estado de uma cadeia de Markov.transition_counter) para simular transições de probabilidade.

4. Geração de sinais de negociação: com base no estado atual, a estratégia gera sinais de compra, venda ou fechamento. Inicia uma posição longa quando o estado é de alta, uma posição curta quando de baixa e fecha todas as posições quando estagnado.

Vantagens da estratégia

1. Modelo probabilístico: Ao incorporar o modelo da cadeia de Markov, a estratégia pode capturar melhor a aleatoriedade e a incerteza do mercado, o que é desafiador para os métodos tradicionais de análise técnica.

2. Flexibilidade: a estratégia pode ser adaptada a diferentes ambientes de mercado ajustando os parâmetros de probabilidade de transição, conferindo-lhe uma forte adaptabilidade.

3. Consideração de vários estados: em comparação com as estratégias simples de tendência, esta estratégia considera três estados de mercado (bullish, bearish, stagnant), proporcionando uma compreensão mais abrangente da dinâmica do mercado.

4. Gestão de riscos: ao fechar posições em estado de estagnação, a estratégia incorpora um mecanismo de gestão de riscos integrado, ajudando a controlar perdas potenciais.

5. Interpretabilidade: Apesar de usar um modelo de probabilidade, a lógica da estratégia é relativamente simples e direta, tornando-a fácil de entender e ajustar para os traders.

Riscos estratégicos

1. Sensibilidade dos parâmetros: o desempenho da estratégia depende fortemente dos parâmetros de probabilidade de transição definidos.

2. A estratégia baseia os julgamentos do Estado nos preços de fechamento, podendo haver alguma latência, potencialmente faltando pontos de viragem importantes em mercados em rápida mudança.

3. Simplificação excessiva: Embora o modelo da cadeia de Markov possa capturar algumas dinâmicas de mercado, ainda é uma simplificação de mercados financeiros complexos e pode ignorar alguns fatores importantes do mercado.

4. Negociação frequente: com base em mudanças frequentes de estado, a estratégia pode gerar sinais comerciais excessivos, aumentando os custos de transação.

5. Adaptabilidade ao mercado: a estratégia pode apresentar um desempenho inferior em determinadas condições de mercado (como mercados com tendências de longo prazo ou mercados altamente voláteis).

Orientações para a otimização da estratégia

1. Introduzir mais estados: considerar a introdução de mais estados de mercado, tais como tendência de alta forte, tendência de alta fraca, etc., para descrever melhor a dinâmica do mercado.

2. Ajuste dinâmico da probabilidade: desenvolver um mecanismo para ajustar dinamicamente as probabilidades de transição com base no desempenho recente do mercado, tornando a estratégia mais adaptável.

3. Integrar outros indicadores técnicos: Incorporar indicadores técnicos tradicionais como médias móveis, RSI, etc., na lógica de julgamento do estado para melhorar a precisão da previsão.

4. Otimizar a lógica do julgamento do estado: Use uma lógica mais complexa para julgar os estados do mercado, como considerar os movimentos de preços em vários períodos de tempo.

5. Introduzir Stop-Loss e Take-Profit: adicionar mecanismos de stop-loss e take-profit à estratégia para controlar ainda mais o risco e bloquear os lucros.

6. Backtesting e Optimização de Parâmetros: Realizar backtesting em larga escala da estratégia, usando métodos como algoritmos genéticos para otimizar parâmetros de probabilidade de transição.

7. Considerar os custos de transação: Incorporar a consideração dos custos de transação na lógica da estratégia para evitar negociações excessivamente frequentes.

Conclusão

A Estratégia de Negociação Quantitativa de Estado de Transição da Cadeia de Probabilidade de Markov é um método de negociação inovador que combina inteligentemente modelos de probabilidade com análise técnica tradicional.

Embora a estratégia tenha riscos como sensibilidade de parâmetros e potencial simplificação excessiva, sua flexibilidade e interpretabilidade a tornam uma ferramenta de negociação promissora.

Para os traders, esta estratégia fornece uma nova perspectiva sobre como usar modelos de probabilidade para entender e prever o comportamento do mercado.