The resource loading... loading...

Dynamic RSI Oscillator Polynomial Fitting Indicator Trend Quantitative Trading Strategy

Author: ChaoZhang, Date: 2024-12-11 15:32:23
Tags: RSIDRSIQREMARMSEMSE

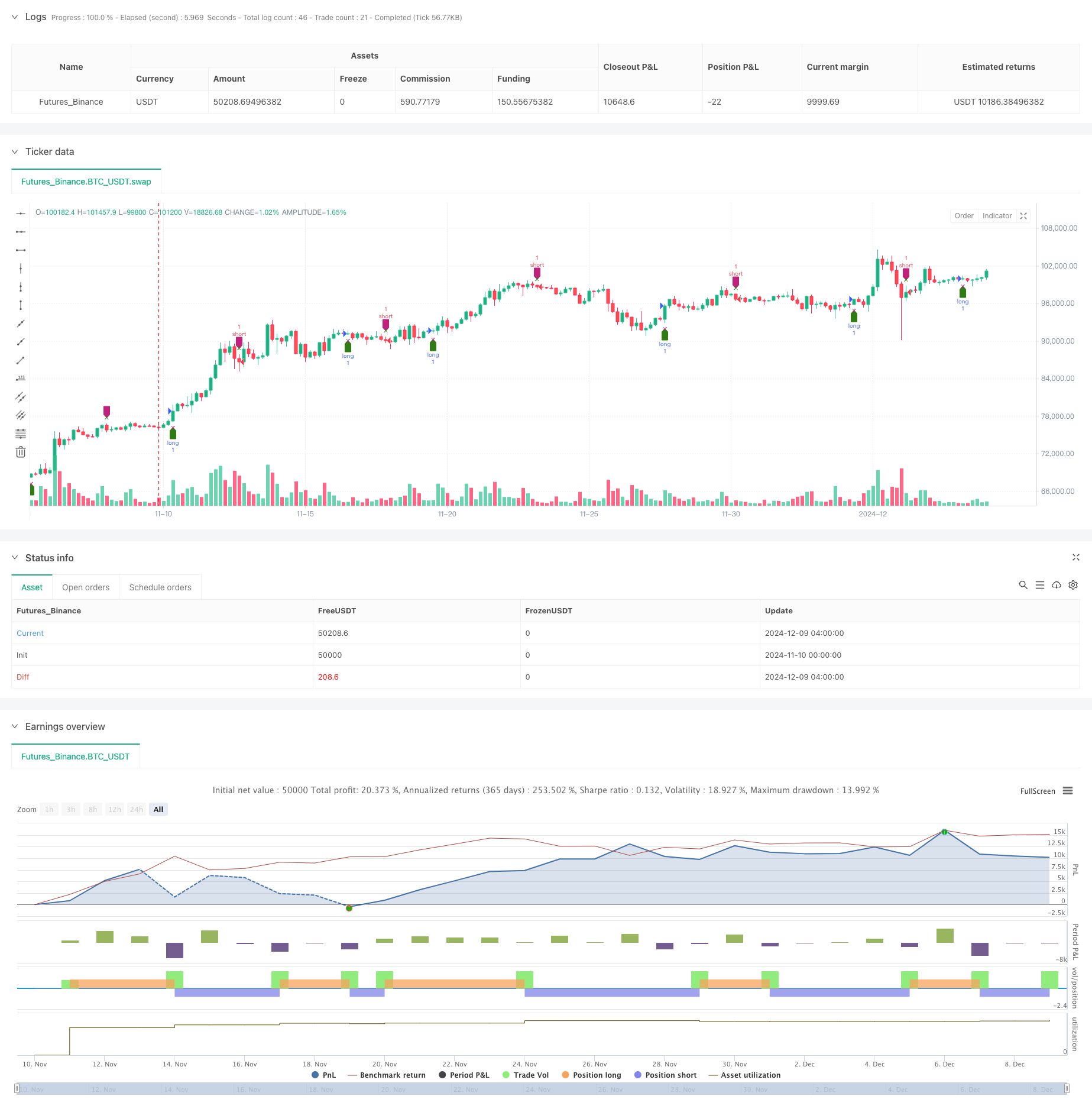
This strategy is a quantitative trading system based on RSI dynamic oscillator. By performing polynomial fitting and time series analysis on the RSI indicator, it calculates the rate of change of RSI to capture market momentum. The strategy uses advanced mathematical methods such as QR decomposition for signal processing and combines with moving average system for trading decisions.

Strategy Principle

The core of the strategy is the Delta-RSI oscillator, which is implemented through the following steps:

First calculate traditional RSI indicator as basic data
Use polynomial fitting to smooth RSI and reduce noise
Calculate time derivative of RSI to get Delta-RSI, reflecting rate of change of RSI
Compare Delta-RSI with its moving average to generate trading signals
Use root mean square error (RMSE) to evaluate and filter fitting quality

Trading signals can be generated in three ways:

Zero-line crossing: Long when Delta-RSI turns positive from negative, short when turns negative from positive
Signal line crossing: Long/short when Delta-RSI crosses above/below its moving average
Direction change: Long when Delta-RSI starts rising in negative territory, short when starts falling in positive territory

Strategy Advantages

Solid mathematical foundation: Uses advanced mathematical methods like QR decomposition for signal processing
Signal smoothing: Polynomial fitting can effectively filter market noise and improve signal quality
High flexibility: Provides multiple signal generation methods and parameter choices to adapt to different market conditions
Controllable risk: Includes RMSE filtering mechanism to screen out more reliable signals
Computational efficiency: Matrix operations use optimized algorithms for high running efficiency

Strategy Risks

Parameter sensitivity: Multiple key parameters need careful adjustment, poor parameter selection seriously affects strategy performance
Lag: Signal smoothing introduces some delay, may miss rapid market moves
False breakouts: May generate false signals in oscillating markets, increasing trading costs
Computational complexity: Involves many matrix operations, may have performance bottlenecks in high-frequency trading
Overfitting: Need to avoid overfitting historical data when optimizing parameters

Strategy Optimization Directions

Adaptive parameters: Dynamically adjust RSI period and fitting order based on market volatility
Multiple timeframes: Incorporate signals from more timeframes for cross-validation
Volatility filtering: Add volatility indicators like ATR for signal filtering
Market classification: Use different signal generation rules for different market states (trend/oscillation)
Stop-loss optimization: Add smarter stop-loss mechanisms, like dynamic stops based on support/resistance levels

Summary

This is a complete quantitative trading strategy with solid theoretical foundation. Through analysis of RSI’s dynamic characteristics combined with modern mathematical methods for signal processing, it can effectively capture market trends. While there are some issues with parameter sensitivity and computational complexity, the strategy has good practical value through proper parameter selection and optimization improvements. When applying to live trading, it’s recommended to pay attention to risk control, set reasonable position sizes, and continuously monitor strategy performance.

/*backtest
start: 2024-11-10 00:00:00
end: 2024-12-09 08:00:00
period: 4h
basePeriod: 4h
exchanges: [{"eid":"Futures_Binance","currency":"BTC_USDT"}]
*/

// This source code is subject to the terms of the Mozilla Public License 2.0 at https://mozilla.org/MPL/2.0/
// © tbiktag
//
// Delta-RSI Oscillator Strategy
//
// A strategy that uses Delta-RSI Oscillator (© tbiktag) as a stand-alone indicator:
// https://www.tradingview.com/script/OXQVFTQD-Delta-RSI-Oscillator/
//
// Delta-RSI is a smoothed time derivative of the RSI, plotted as a histogram 
// and serving as a momentum indicator. 
// 
// Input parameters:
// RSI Length: The timeframe of the RSI that serves as an input to D-RSI.
// Length: The length of the lookback frame used for local regression.
// Polynomial Order: The order of the local polynomial function used to interpolate the RSI.
// Signal Length: The length of a EMA of the D-RSI series that is used as a signal line.
// Trade signals are generated based on three optional conditions:
// - Zero-crossing: bullish when D-RSI crosses zero from negative to positive values (bearish otherwise)
// - Signal Line Crossing: bullish when D-RSI crosses from below to above the signal line (bearish otherwise)
// - Direction Change: bullish when D-RSI was negative and starts ascending (bearish otherwise)
//
// Since D-RSI oscillator is based on polynomial fitting of the RSI curve, there is also an option
// to filter trade signal by means of the root mean-square error of the fit (normalized by the sample average).
// 
//@version=5
strategy(title='Delta-RSI Oscillator Strategy-QuangVersion', shorttitle='D-RSI-Q', overlay=true)

// ---Subroutines---
matrix_get(_A, _i, _j, _nrows) =>
    // Get the value of the element of an implied 2d matrix
    //input: 
    // _A :: array: pseudo 2d matrix _A = [[column_0],[column_1],...,[column_(n-1)]]
    // _i :: integer: row number
    // _j :: integer: column number
    // _nrows :: integer: number of rows in the implied 2d matrix
    array.get(_A, _i + _nrows * _j)

matrix_set(_A, _value, _i, _j, _nrows) =>
    // Set a value to the element of an implied 2d matrix
    //input: 
    // _A :: array, changed on output: pseudo 2d matrix _A = [[column_0],[column_1],...,[column_(n-1)]]
    // _value :: float: the new value to be set
    // _i :: integer: row number
    // _j :: integer: column number
    // _nrows :: integer: number of rows in the implied 2d matrix
    array.set(_A, _i + _nrows * _j, _value)

transpose(_A, _nrows, _ncolumns) =>
    // Transpose an implied 2d matrix
    // input:
    // _A :: array: pseudo 2d matrix _A = [[column_0],[column_1],...,[column_(n-1)]]
    // _nrows :: integer: number of rows in _A
    // _ncolumns :: integer: number of columns in _A
    // output:
    // _AT :: array: pseudo 2d matrix with implied dimensions: _ncolums x _nrows
    var _AT = array.new_float(_nrows * _ncolumns, 0)
    for i = 0 to _nrows - 1 by 1
        for j = 0 to _ncolumns - 1 by 1
            matrix_set(_AT, matrix_get(_A, i, j, _nrows), j, i, _ncolumns)
    _AT

multiply(_A, _B, _nrowsA, _ncolumnsA, _ncolumnsB) =>
    // Calculate scalar product of two matrices
    // input: 
    // _A :: array: pseudo 2d matrix
    // _B :: array: pseudo 2d matrix
    // _nrowsA :: integer: number of rows in _A
    // _ncolumnsA :: integer: number of columns in _A
    // _ncolumnsB :: integer: number of columns in _B
    // output:
    // _C:: array: pseudo 2d matrix with implied dimensions _nrowsA x _ncolumnsB
    var _C = array.new_float(_nrowsA * _ncolumnsB, 0)
    int _nrowsB = _ncolumnsA
    float elementC = 0.0
    for i = 0 to _nrowsA - 1 by 1
        for j = 0 to _ncolumnsB - 1 by 1
            elementC := 0
            for k = 0 to _ncolumnsA - 1 by 1
                elementC += matrix_get(_A, i, k, _nrowsA) * matrix_get(_B, k, j, _nrowsB)
                elementC
            matrix_set(_C, elementC, i, j, _nrowsA)
    _C

vnorm(_X, _n) =>
    //Square norm of vector _X with size _n
    float _norm = 0.0
    for i = 0 to _n - 1 by 1
        _norm += math.pow(array.get(_X, i), 2)
        _norm
    math.sqrt(_norm)

qr_diag(_A, _nrows, _ncolumns) =>
    //QR Decomposition with Modified Gram-Schmidt Algorithm (Column-Oriented)
    // input:
    // _A :: array: pseudo 2d matrix _A = [[column_0],[column_1],...,[column_(n-1)]]
    // _nrows :: integer: number of rows in _A
    // _ncolumns :: integer: number of columns in _A
    // output:
    // _Q: unitary matrix, implied dimenstions _nrows x _ncolumns
    // _R: upper triangular matrix, implied dimansions _ncolumns x _ncolumns
    var _Q = array.new_float(_nrows * _ncolumns, 0)
    var _R = array.new_float(_ncolumns * _ncolumns, 0)
    var _a = array.new_float(_nrows, 0)
    var _q = array.new_float(_nrows, 0)
    float _r = 0.0
    float _aux = 0.0
    //get first column of _A and its norm:
    for i = 0 to _nrows - 1 by 1
        array.set(_a, i, matrix_get(_A, i, 0, _nrows))
    _r := vnorm(_a, _nrows)
    //assign first diagonal element of R and first column of Q
    matrix_set(_R, _r, 0, 0, _ncolumns)
    for i = 0 to _nrows - 1 by 1
        matrix_set(_Q, array.get(_a, i) / _r, i, 0, _nrows)
    if _ncolumns != 1
        //repeat for the rest of the columns
        for k = 1 to _ncolumns - 1 by 1
            for i = 0 to _nrows - 1 by 1
                array.set(_a, i, matrix_get(_A, i, k, _nrows))
            for j = 0 to k - 1 by 1
                //get R_jk as scalar product of Q_j column and A_k column:
                _r := 0
                for i = 0 to _nrows - 1 by 1
                    _r += matrix_get(_Q, i, j, _nrows) * array.get(_a, i)
                    _r
                matrix_set(_R, _r, j, k, _ncolumns)
                //update vector _a
                for i = 0 to _nrows - 1 by 1
                    _aux := array.get(_a, i) - _r * matrix_get(_Q, i, j, _nrows)
                    array.set(_a, i, _aux)
            //get diagonal R_kk and Q_k column
            _r := vnorm(_a, _nrows)
            matrix_set(_R, _r, k, k, _ncolumns)
            for i = 0 to _nrows - 1 by 1
                matrix_set(_Q, array.get(_a, i) / _r, i, k, _nrows)
    [_Q, _R]

pinv(_A, _nrows, _ncolumns) =>
    //Pseudoinverse of matrix _A calculated using QR decomposition
    // Input: 
    // _A:: array: implied as a (_nrows x _ncolumns) matrix _A = [[column_0],[column_1],...,[column_(_ncolumns-1)]]
    // Output: 
    // _Ainv:: array implied as a (_ncolumns x _nrows) matrix _A = [[row_0],[row_1],...,[row_(_nrows-1)]]
    // ----
    // First find the QR factorization of A: A = QR,
    // where R is upper triangular matrix.
    // Then _Ainv = R^-1*Q^T.
    // ----
    [_Q, _R] = qr_diag(_A, _nrows, _ncolumns)
    _QT = transpose(_Q, _nrows, _ncolumns)
    // Calculate Rinv:
    var _Rinv = array.new_float(_ncolumns * _ncolumns, 0)
    float _r = 0.0
    matrix_set(_Rinv, 1 / matrix_get(_R, 0, 0, _ncolumns), 0, 0, _ncolumns)
    if _ncolumns != 1
        for j = 1 to _ncolumns - 1 by 1
            for i = 0 to j - 1 by 1
                _r := 0.0
                for k = i to j - 1 by 1
                    _r += matrix_get(_Rinv, i, k, _ncolumns) * matrix_get(_R, k, j, _ncolumns)
                    _r
                matrix_set(_Rinv, _r, i, j, _ncolumns)
            for k = 0 to j - 1 by 1
                matrix_set(_Rinv, -matrix_get(_Rinv, k, j, _ncolumns) / matrix_get(_R, j, j, _ncolumns), k, j, _ncolumns)
            matrix_set(_Rinv, 1 / matrix_get(_R, j, j, _ncolumns), j, j, _ncolumns)
    //
    _Ainv = multiply(_Rinv, _QT, _ncolumns, _ncolumns, _nrows)
    _Ainv

norm_rmse(_x, _xhat) =>
    // Root Mean Square Error normalized to the sample mean
    // _x.   :: array float, original data
    // _xhat :: array float, model estimate
    // output
    // _nrmse:: float
    float _nrmse = 0.0
    if array.size(_x) != array.size(_xhat)
        _nrmse := na
        _nrmse
    else
        int _N = array.size(_x)
        float _mse = 0.0
        for i = 0 to _N - 1 by 1
            _mse += math.pow(array.get(_x, i) - array.get(_xhat, i), 2) / _N
            _mse
        _xmean = array.sum(_x) / _N
        _nrmse := math.sqrt(_mse) / _xmean
        _nrmse
    _nrmse


diff(_src, _window, _degree) =>
    // Polynomial differentiator
    // input:
    // _src:: input series
    // _window:: integer: wigth of the moving lookback window
    // _degree:: integer: degree of fitting polynomial
    // output:
    // _diff :: series: time derivative
    // _nrmse:: float: normalized root mean square error
    //
    // Vandermonde matrix with implied dimensions (window x degree+1)
    // Linear form: J = [ [z]^0, [z]^1, ... [z]^degree], with z = [ (1-window)/2 to (window-1)/2 ] 
    var _J = array.new_float(_window * (_degree + 1), 0)
    for i = 0 to _window - 1 by 1
        for j = 0 to _degree by 1
            matrix_set(_J, math.pow(i, j), i, j, _window)
    // Vector of raw datapoints:
    var _Y_raw = array.new_float(_window, na)
    for j = 0 to _window - 1 by 1
        array.set(_Y_raw, j, _src[_window - 1 - j])
    // Calculate polynomial coefficients which minimize the loss function
    _C = pinv(_J, _window, _degree + 1)
    _a_coef = multiply(_C, _Y_raw, _degree + 1, _window, 1)
    // For first derivative, approximate the last point (i.e. z=window-1) by 
    float _diff = 0.0
    for i = 1 to _degree by 1
        _diff += i * array.get(_a_coef, i) * math.pow(_window - 1, i - 1)
        _diff
    // Calculates data estimate (needed for rmse)
    _Y_hat = multiply(_J, _a_coef, _window, _degree + 1, 1)
    float _nrmse = norm_rmse(_Y_raw, _Y_hat)
    [_diff, _nrmse]

/// --- main ---
degree = input.int(title='Polynomial Order', group='Model Parameters:', inline='linepar1', defval=2, minval=1)
rsi_l = input.int(title='RSI Length', group='Model Parameters:', inline='linepar1', defval=21, minval=1, tooltip='The period length of RSI that is used as input.')
window = input.int(title='Length ( > Order)', group='Model Parameters:', inline='linepar2', defval=21, minval=2)
signalLength = input.int(title='Signal Length', group='Model Parameters:', inline='linepar2', defval=9, tooltip='The signal line is a EMA of the D-RSI time series.')
islong = input.bool(title='Buy', group='Show Signals:', inline='lineent', defval=true)
isshort = input.bool(title='Sell', group='Show Signals:', inline='lineent', defval=true)
showendlabels = input.bool(title='Exit', group='Show Signals:', inline='lineent', defval=true)
buycond = input.string(title='Buy', group='Entry and Exit Conditions:', inline='linecond', defval='Zero-Crossing', options=['Zero-Crossing', 'Signal Line Crossing', 'Direction Change'])
sellcond = input.string(title='Sell', group='Entry and Exit Conditions:', inline='linecond', defval='Zero-Crossing', options=['Zero-Crossing', 'Signal Line Crossing', 'Direction Change'])
endcond = input.string(title='Exit', group='Entry and Exit Conditions:', inline='linecond', defval='Zero-Crossing', options=['Zero-Crossing', 'Signal Line Crossing', 'Direction Change'])
usenrmse = input.bool(title='', group='Filter by Means of Root-Mean-Square Error of RSI Fitting:', inline='linermse', defval=false)
rmse_thrs = input.float(title='RSI fitting Error Threshold, %', group='Filter by Means of Root-Mean-Square Error of RSI Fitting:', inline='linermse', defval=10, minval=0.0) / 100


src = ta.rsi(close, rsi_l)
[drsi, nrmse] = diff(src, window, degree)
signalline = ta.ema(drsi, signalLength)

// Conditions and filters
filter_rmse = usenrmse ? nrmse < rmse_thrs : true
dirchangeup = drsi > drsi[1] and drsi[1] < drsi[2] and drsi[1] < 0.0
dirchangedw = drsi < drsi[1] and drsi[1] > drsi[2] and drsi[1] > 0.0
crossup = ta.crossover(drsi, 0.0)
crossdw = ta.crossunder(drsi, 0.0)
crosssignalup = ta.crossover(drsi, signalline)
crosssignaldw = ta.crossunder(drsi, signalline)

//Signals
golong = (buycond == 'Direction Change' ? dirchangeup : buycond == 'Zero-Crossing' ? crossup : crosssignalup) and filter_rmse
goshort = (sellcond == 'Direction Change' ? dirchangedw : sellcond == 'Zero-Crossing' ? crossdw : crosssignaldw) and filter_rmse
endlong = (endcond == 'Direction Change' ? dirchangedw : endcond == 'Zero-Crossing' ? crossdw : crosssignaldw) and filter_rmse
endshort = (endcond == 'Direction Change' ? dirchangeup : endcond == 'Zero-Crossing' ? crossup : crosssignalup) and filter_rmse
plotshape(golong and islong ? low : na, location=location.belowbar, style=shape.labelup, color=color.new(#2E7C13, 0), size=size.small, title='Buy')
plotshape(goshort and isshort ? high : na, location=location.abovebar, style=shape.labeldown, color=color.new(#BF217C, 0), size=size.small, title='Sell')
plotshape(showendlabels and endlong and islong ? high : na, location=location.abovebar, style=shape.xcross, color=color.new(#2E7C13, 0), size=size.tiny, title='Exit Long')
plotshape(showendlabels and endshort and isshort ? low : na, location=location.belowbar, style=shape.xcross, color=color.new(#BF217C, 0), size=size.tiny, title='Exit Short')

alertcondition(golong, title='Long Signal', message='D-RSI: Long Signal')
alertcondition(goshort, title='Short Signal', message='D-RSI: Short Signal')
alertcondition(endlong, title='Exit Long Signal', message='D-RSI: Exit Long')
alertcondition(endshort, title='Exit Short Signal', message='D-RSI: Exit Short')

strategy.entry('long', strategy.long, when=golong and islong)
strategy.entry('short', strategy.short, when=goshort and isshort)
strategy.close('long', when=endlong and islong)
strategy.close('short', when=endshort and isshort)

Related

More

Forums
|
API
|
Github
|
About
|
SiteMap