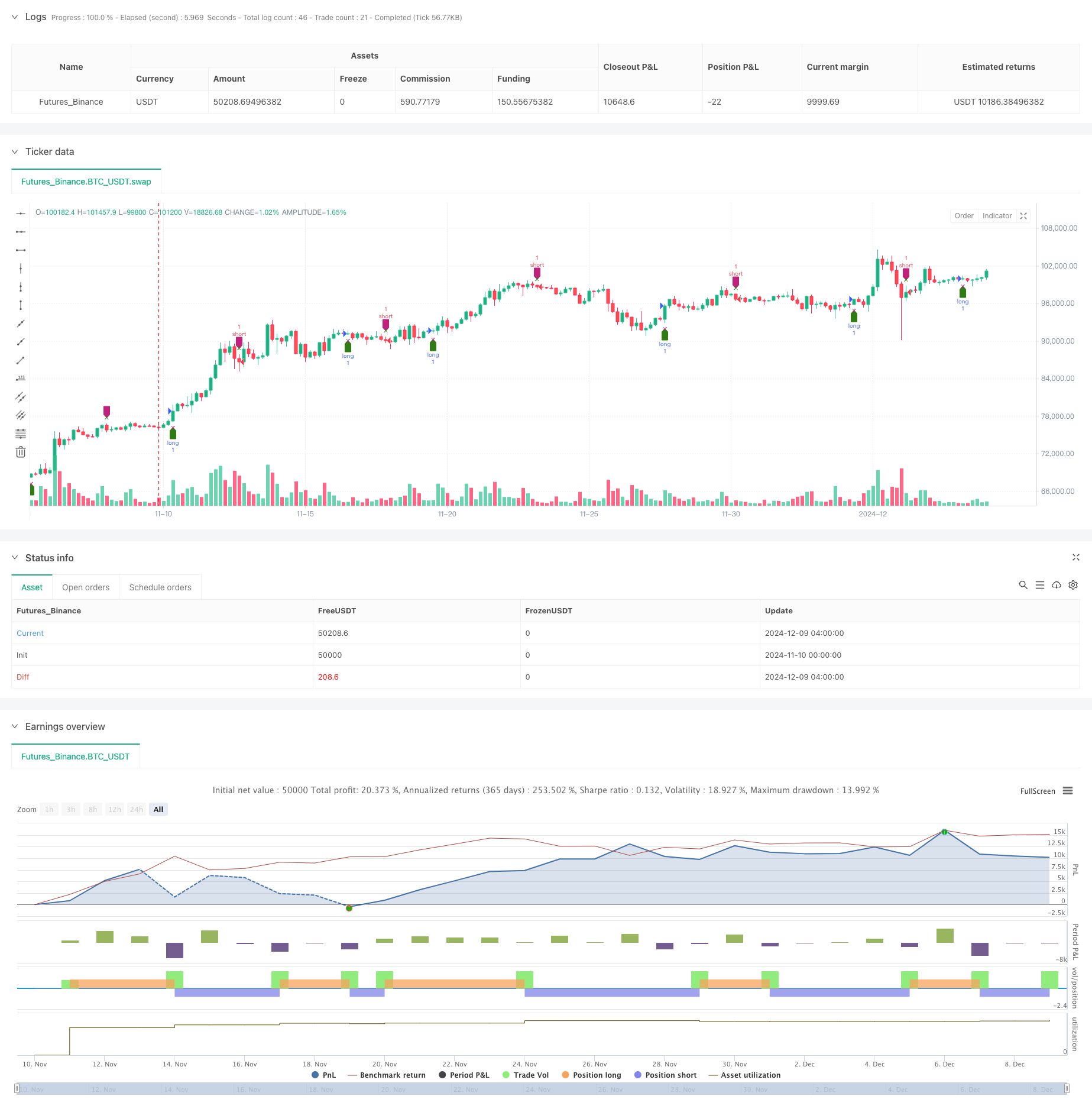
Chiến lược này là một hệ thống giao dịch định lượng dựa trên dao động động RSI. Bằng cách thực hiện phân tích chuỗi thời gian và hợp nhất đa phương thức của chỉ số RSI, tính toán tỷ lệ thay đổi của RSI để nắm bắt động lực thị trường. Chiến lược sử dụng các phương pháp toán học cao cấp như phân tích QR để xử lý tín hiệu và kết hợp với hệ thống thống nhất để đưa ra quyết định giao dịch.

Nguyên tắc chiến lược

Trung tâm của chiến lược là dao động Delta-RSI, được thực hiện thông qua các bước sau:

1. Đầu tiên, tính toán chỉ số RSI truyền thống như một dữ liệu cơ bản.
2. RSI được xử lý trơn tru, giảm tiếng ồn bằng cách sử dụng sự phù hợp đa dạng
3. Tính biến thời gian của RSI được lấy từ Delta-RSI, phản ánh tốc độ thay đổi của RSI
4. So sánh Delta-RSI với đường trung bình di chuyển của nó để tạo ra tín hiệu giao dịch
5. Đánh giá và lọc chất lượng phù hợp bằng cách sử dụng sai sót gốc đồng phương ((RMSE)

Các tín hiệu giao dịch có thể được tạo ra theo ba cách:

• Đi ngang 0: Delta-RSI tăng khi chuyển từ giá trị âm, giảm khi chuyển từ giá trị dương
• Giao lộ tín hiệu: Delta-RSI tăng/giảm khi vượt qua đường trung bình di chuyển của nó
• Thay đổi hướng: Delta-RSI làm nhiều khi vùng giá âm bắt đầu tăng, làm trống khi vùng giá dương bắt đầu giảm

Lợi thế chiến lược

1. Cơ sở toán học vững chắc: sử dụng phương pháp toán học cao cấp như phân giải QR để xử lý tín hiệu, cơ sở lý thuyết đáng tin cậy
2. Tín hiệu mượt mà: Kết hợp đa dạng có thể lọc hiệu quả tiếng ồn thị trường, cải thiện chất lượng tín hiệu
3. Tính linh hoạt: cung cấp nhiều phương thức tạo tín hiệu và tùy chọn tham số để thích ứng với các môi trường thị trường khác nhau
4. Kiểm soát rủi ro: Bao gồm cơ chế lọc RMSE, có thể lọc các tín hiệu có độ tin cậy cao hơn
5. Hiệu quả tính toán: Máy tính toán ma trận sử dụng các thuật toán tối ưu hóa, hoạt động hiệu quả hơn

Rủi ro chiến lược

1. Nhận định tham số: Nhiều tham số quan trọng cần được điều chỉnh kỹ lưỡng, lựa chọn tham số không đúng cách có thể ảnh hưởng nghiêm trọng đến hiệu suất của chiến lược
2. Sự chậm trễ: xử lý tín hiệu trơn tru sẽ dẫn đến sự chậm trễ, có thể bỏ lỡ tốc độ nhanh
3. Phá vỡ giả: có thể tạo ra tín hiệu giả trong thị trường biến động, làm tăng chi phí giao dịch
4. Tính toán phức tạp: liên quan đến nhiều hoạt động ma trận, có thể có sự tắc nghẽn về hiệu suất trong giao dịch tần số cao
5. Quá phù hợp: Chú ý tránh quá phù hợp với dữ liệu lịch sử khi tối ưu hóa tham số

Hướng tối ưu hóa chiến lược

1. Các tham số tự điều chỉnh: có thể điều chỉnh chu kỳ RSI và số bậc phù hợp theo biến động của thị trường
2. Nhiều chu kỳ thời gian: tín hiệu kết hợp nhiều chu kỳ thời gian được kiểm tra chéo
3. Bộ lọc tỷ lệ dao động: thêm các chỉ số tỷ lệ dao động như ATR để lọc tín hiệu
4. Phân loại thị trường: sử dụng các quy tắc tạo tín hiệu khác nhau cho các tình trạng thị trường khác nhau (trend / oscillation)
5. Tối ưu hóa dừng lỗ: thêm các cơ chế dừng lỗ thông minh hơn, chẳng hạn như dừng động dựa trên điểm kháng cự hỗ trợ

Tóm tắt

Đây là một chiến lược giao dịch định lượng có cấu trúc đầy đủ, nền tảng lý thuyết vững chắc. Bằng cách phân tích tính năng động của RSI, kết hợp với phương pháp toán học hiện đại để xử lý tín hiệu, có thể nắm bắt được xu hướng thị trường tốt hơn. Mặc dù có một số vấn đề về độ nhạy cảm và tính toán phức tạp, nhưng chiến lược này có giá trị ứng dụng tốt thông qua lựa chọn và tối ưu hóa tham số hợp lý.